


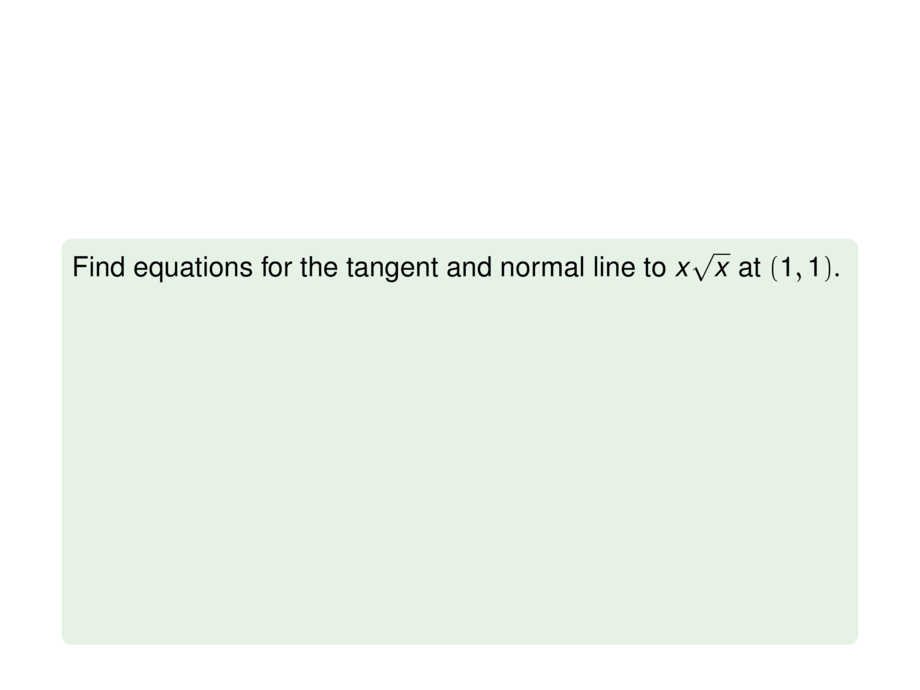
































































































21/81
\begin{frame}
\frametitle{Derivatives of Basic Functions}
\begin{block}{}
The \emph{normal line} is perpendicular to the tangent.\pause\medskip
If the tangent has slope $m$, then the normal line has slope $-\frac{1}{m}$.
\end{block}
\pause
\begin{exampleblock}{}
Find equations for the tangent and normal line to $x\sqrt{x}$ at $(1,1)$.
\pause
\begin{talign}
f'(x) = \frac{d}{dx}(x\sqrt{x}) \mpause[1]{ = \frac{d}{dx}(x^{1.5})} \mpause[2]{= 1.5 x^{.5}} \mpause[3]{= \frac{3}{2} \sqrt{x}}
\end{talign}
\pause\pause\pause\pause
The slope of the tangent at $(1,1)$ is $\frac{3}{2}$. \pause Hence the tangent is
\begin{talign}
y - 1= \frac{3}{2} (x-1) && y = \frac{3}{2} x - \frac{1}{2}
\end{talign}
\pause
The slope of the normal at $(1,1)$ is $-1/\frac{3}{2} = -\frac{2}{3}$. \pause Hence the normal is
\begin{talign}
y - 1= -\frac{2}{3} (x-1) && y = -\frac{2}{3} x + \frac{5}{3}
\end{talign}
\end{exampleblock}
\end{frame}

