




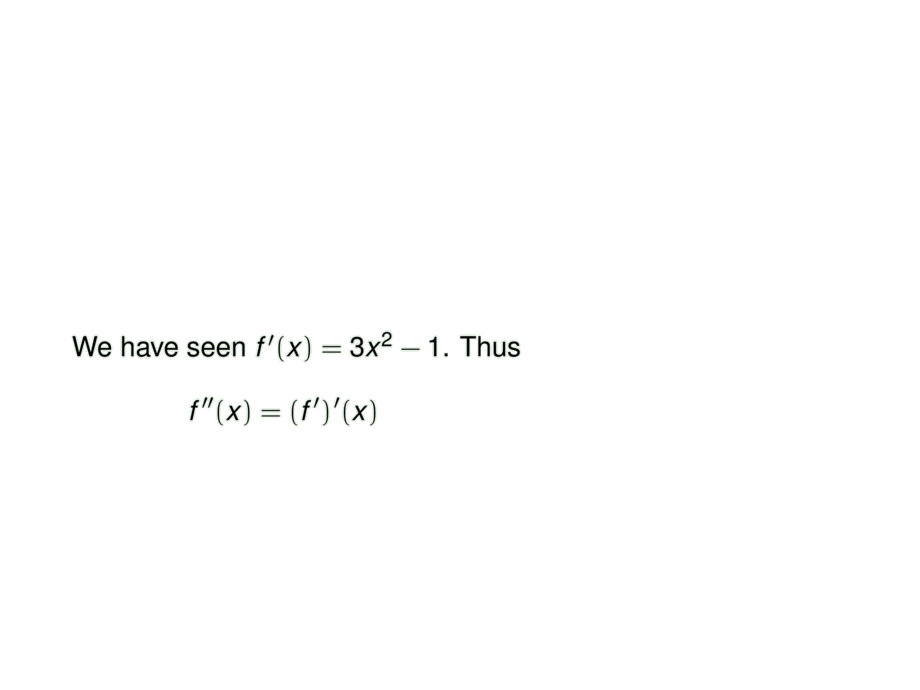

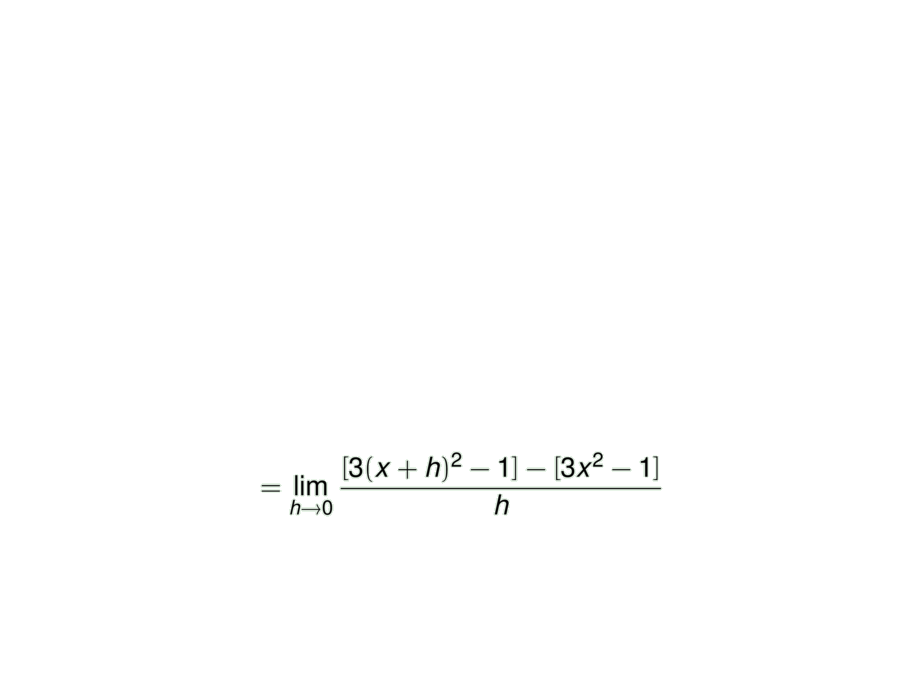




























































































94/116
\begin{frame}
\frametitle{Higher Derivatives}
If $f$ is a function,
the derivative $f'$ is also a function.
\pause\medskip
Thus we can compute the derivative of the derivative:
\begin{talign}
(f')' = f''
\end{talign}
\pause
The function $f''$ is called \emph{second derivative} of $f$.
\pause\smallskip
% In Leibnitz notation the second derivative of $y = f(x)$ is written as:
% \begin{talign}
% \frac{d}{dx} \left(\frac{dy}{dx} \right) \;=\; \frac{d^2y}{dx^2}
% \end{talign}
\begin{exampleblock}{}
Let $f(x) = x^3 - x$. Find $f''(x)$.
\pause\medskip
We have seen $f'(x) = 3x^2 - 1$. Thus
\begin{talign}
f''(x) &= (f')'(x) \mpause[1]{= \lim_{h\to 0} \frac{f'(x+h) - f'(x)}{h}}\\
&\mpause[2]{= \lim_{h\to 0} \frac{[3(x+h)^2 - 1] - [3x^2 - 1]}{h}}\\
&\mpause[3]{= \lim_{h\to 0} \frac{3x^2 + 6xh + 3h^2 - 1 - 3x^2 + 1}{h}}\\
&\mpause[4]{= \lim_{h\to 0} \frac{6xh + 3h^2}{h}}
\mpause[5]{= \lim_{h\to 0} (6x + 3h)}
\mpause[6]{= 6x}
\end{talign}
\end{exampleblock}
\end{frame}

