\begin{frame}
  \frametitle{How can a Function fail to be Derivable?}

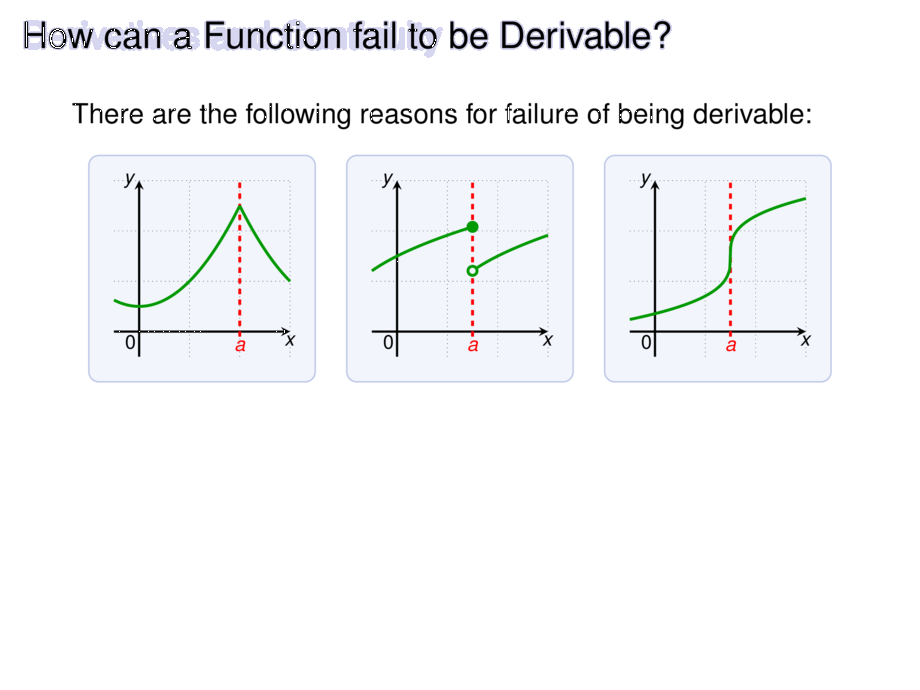
  There are the following reasons for failure of being derivable:
  \begin{center}
  \scalebox{.7}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{3}{-.5}{3}{1}
    \diagramannotatez
    \begin{scope}[ultra thick]
      \draw[cred,dashed] (2,-.1) -- (2,3) node[at start,below] {$a$};
      \draw[cgreen,ultra thick] plot[smooth,domain=-.5:2,samples=20] function{.5*x**2+.5};
      \draw[cgreen,ultra thick] plot[smooth,domain=2:3,samples=20] function{.5*(x-4)**2+.5};
    \end{scope}
  \end{tikzpicture}~\quad~%
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{3}{-.5}{3}{1}
    \diagramannotatez
    \begin{scope}[ultra thick]
      \draw[cred,dashed] (1.5,-.1) -- (1.5,3) node[at start,below] {$a$};
      \draw[cgreen,ultra thick] plot[smooth,domain=-.5:1.5,samples=20] function{sqrt(x+1)+.5};
      \draw[cgreen,ultra thick] plot[smooth,domain=1.5:3,samples=20] function{.5+ sqrt(x-1)};
      \node[include=cgreen] at (1.5,{sqrt(2.5)+.5}) {};
      \node[exclude=cgreen] at (1.5,{.5+ sqrt(.5)}) {};
    \end{scope}
  \end{tikzpicture}~\quad~%
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-.5}{3}{-.5}{3}{1}
    \diagramannotatez
    \begin{scope}[ultra thick]
      \draw[cred,dashed] (1.5,-.1) -- (1.5,3) node[at start,below] {$a$};
      \draw[cgreen,ultra thick] plot[smooth,domain=-.5:3,samples=200] function{1.5+sgn(x-1.5) * abs(x-1.5)**(1./3.)};
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}
  
  \begin{itemize}
    \pause
    \item graph changes direction abruptly (graph has a ``corner'')
    \pause
    \item the function is not continuous at $a$
    \pause
    \item graph has a vertical tangent at $a$, that is:
      \begin{talign}
        \lim_{x\to a} |f'(x)| = \infty
      \end{talign}
      \pause
      Example for a vertical tangent is $f(x) = \sqrt[3]{x}$ at $0$.
  \end{itemize}
\end{frame}