


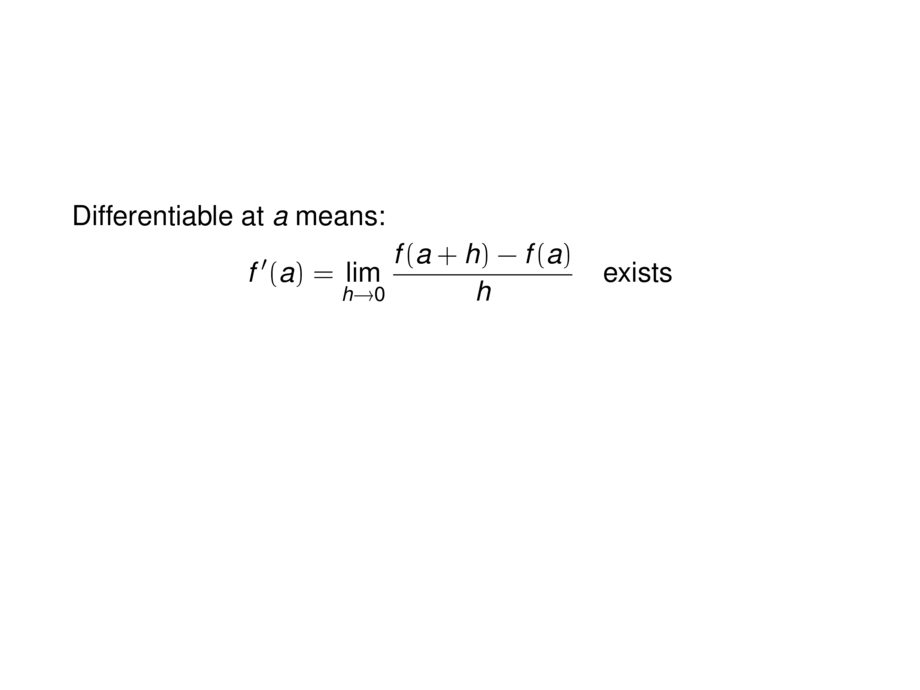

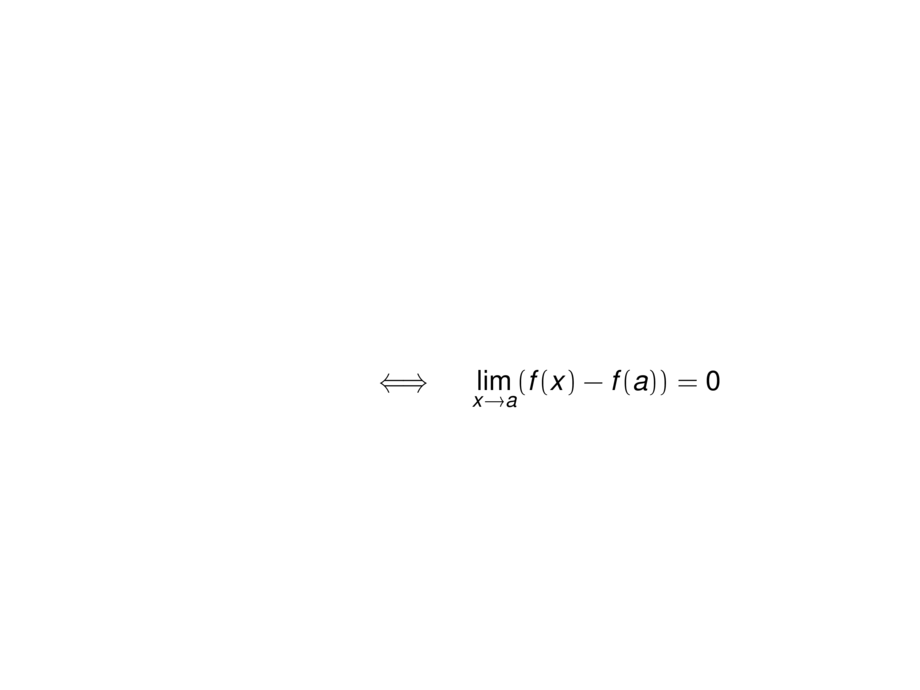






























































































67/116
\begin{frame}
\frametitle{Derivatives and Continuity}
\begin{block}{}
If $f$ is differentiable at $a$, then $f$ is continuous at $a$.
\end{block}
\pause
The proof is in the book. Intuitively it holds because\ldots\hspace{-2ex}
\pause\bigskip
Differentiable at $a$ means:
\begin{talign}
f'(a) = \lim_{h\to 0} \frac{f(a+h) - f(a)}{h} \quad \text{exists}
\end{talign}
\pause
%
Continuous at $a$ means:
\begin{talign}
\lim_{x\to a} f(x) = f(a)
&\mpause[1]{\quad\iff\quad \lim_{x\to a} (f(x) - f(a)) = 0 }\\
&\mpause[2]{\quad\iff\quad \lim_{h\to 0} (f(a+h) - f(a)) = 0 }
\end{talign}
\pause\pause\pause
If the latter limit would not be $0$ (or not exist), \\
then $\frac{f(a+h) - f(a)}{h}$ would get arbitrarily large for small $h$.
\pause
\begin{alertblock}{}
If $f$ is continuous at $a$, then $f$ is \alert{not always} differentiable at $a$.
\end{alertblock}
\pause
E.g. $|x|$ is continuous at $0$ but not differentiable at $0$.
\vspace{10cm}
\end{frame}

