
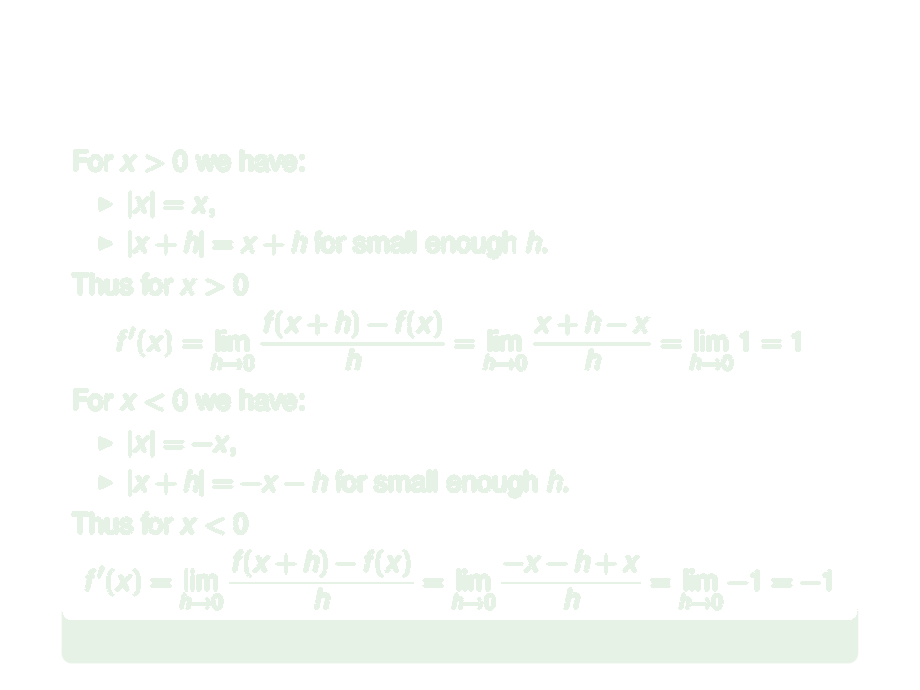
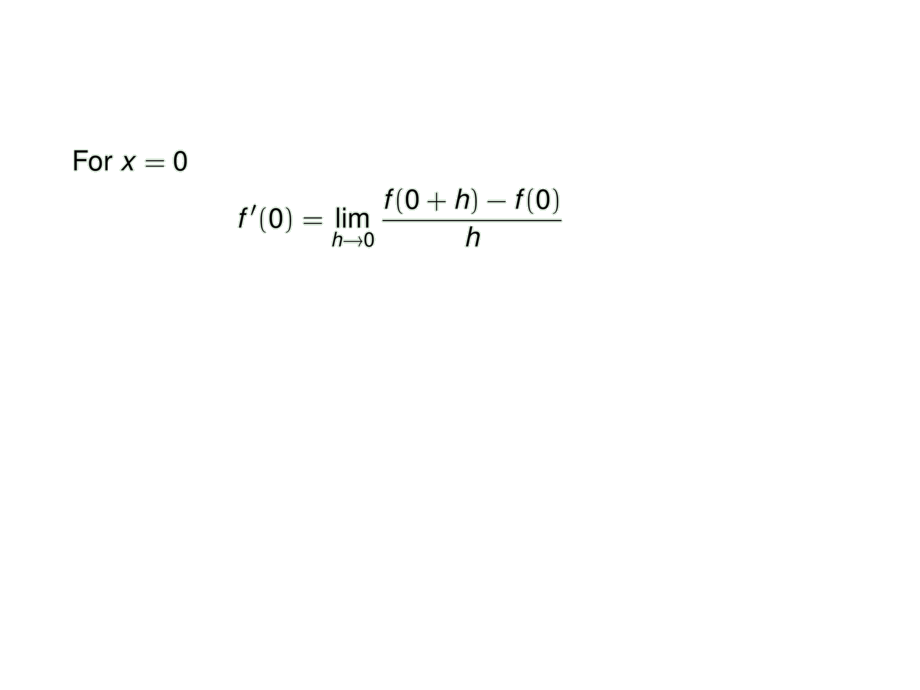


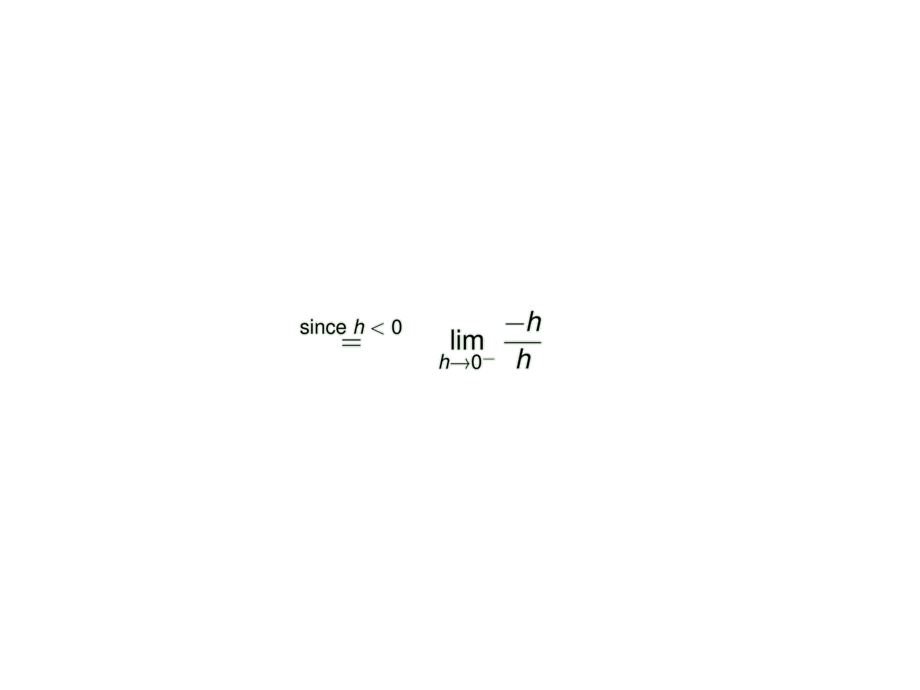

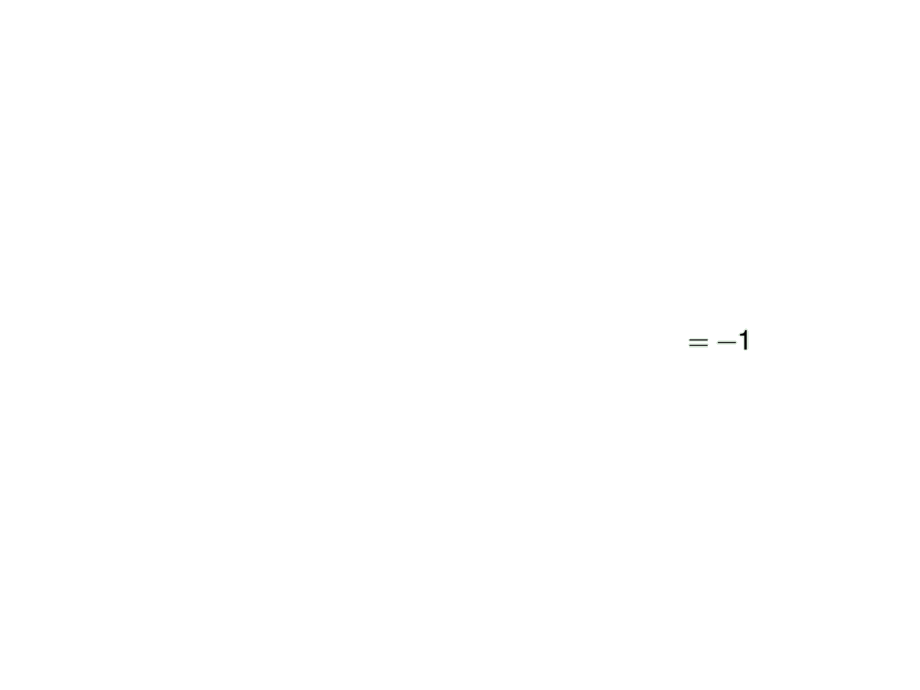
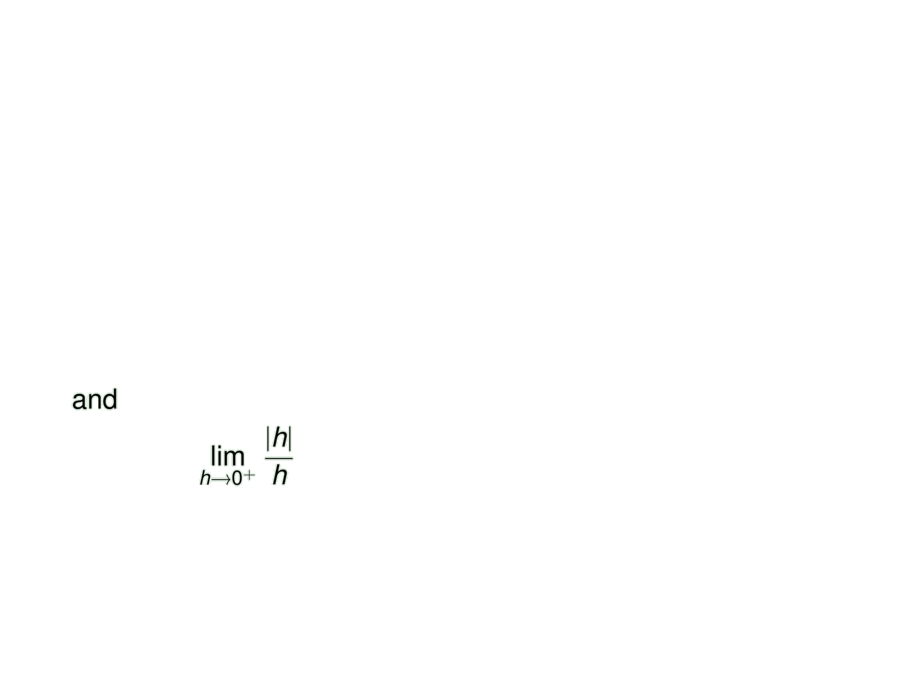



























































































58/116
\begin{frame}
\frametitle{Derivative as a Function}
\begin{exampleblock}{}
Where is $f(x) = |x|$ differentiable?
\pause\medskip
For $x = 0$
\begin{talign}
f'(0) = \lim_{h\to 0} \frac{f(0+h) - f(0)}{h}
\mpause[1]{= \lim_{h\to 0} \frac{|h|}{h}}
\end{talign}
\pause\pause
We need to look at the left and right limits:
\begin{talign}
\lim_{h\to 0^-} \frac{|h|}{h}
&\mpause[1]{\quad\stackrel{\text{since $h < 0$}}{=}\quad \lim_{h\to 0^-} \frac{-h}{h}}
\mpause[2]{= \lim_{h\to 0^-} -1}
\mpause[3]{= -1}
\end{talign}
\pause\pause\pause\pause
and
\begin{talign}
\lim_{h\to 0^+} \frac{|h|}{h}
&\mpause[1]{\quad\stackrel{\text{since $h > 0$}}{=}\quad \lim_{h\to 0^+} \frac{h}{h}}
\mpause[2]{= \lim_{h\to 0^+} 1}
\mpause[3]{= 1}
\end{talign}
\pause\pause\pause\pause
The left and right limits are different.\pause\medskip
Thus $f'(0)$ does not exist, and $f(x)$ is not differentiable at $0$.\pause\medskip
Hence $f$ is differentiable at all numbers in $(-\infty,0) \cup (0,\infty)$.
\end{exampleblock}
\vspace{10cm}
\end{frame}

