\begin{frame}
  \frametitle{Derivative as a Function}

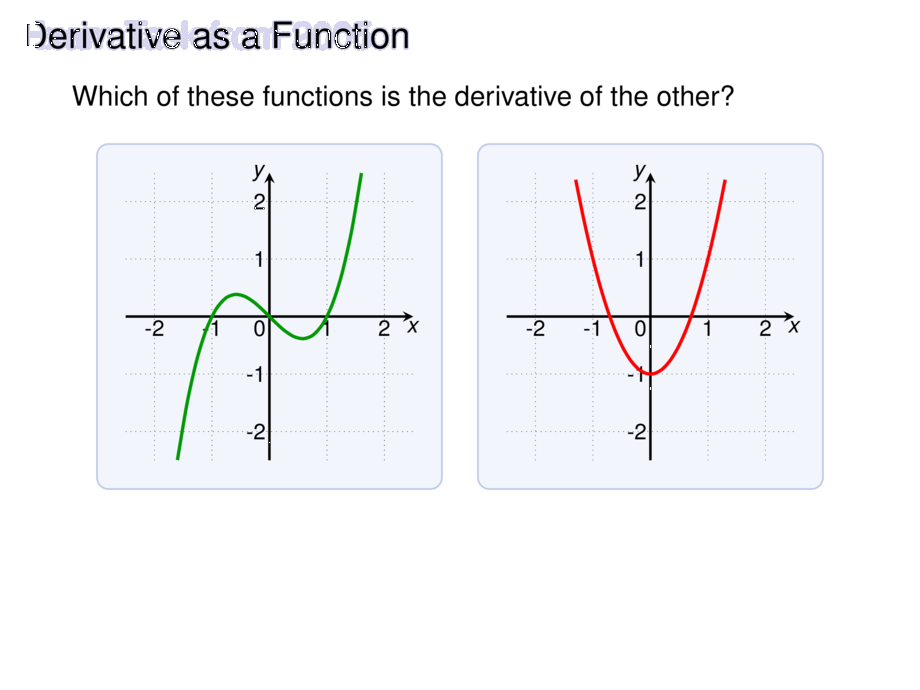
  Which of these functions is the derivative of the other?
  \medskip
  \begin{center}
  \scalebox{.8}{
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-2.5}{2.5}{-2.5}{2.5}{1}
    \diagramannotatez
    \diagramannotatex{-2,-1,1,2}
    \diagramannotatey{-2,-1,1,2}
    \begin{scope}[ultra thick]
      \draw[cgreen,ultra thick] plot[smooth,domain=-1.6:1.6,samples=20] function{x**3 - x};
    \end{scope}
  \end{tikzpicture}~\quad~%
  \begin{tikzpicture}[default,baseline=1cm]
    \diagram{-2.5}{2.5}{-2.5}{2.5}{1}
    \diagramannotatez
    \diagramannotatex{-2,-1,1,2}
    \diagramannotatey{-2,-1,1,2}
    \begin{scope}[ultra thick]
      \draw[cred,ultra thick] plot[smooth,domain=-1.3:1.3,samples=20] function{2*x**2 - 1};
    \end{scope}
  \end{tikzpicture}
  }
  \end{center}
  \pause\medskip
  The right is the derivative of the left:
  \begin{itemize}
  \pause 
    \item look at local maxima and minima of $f$; then $f'$ must be $0$ 
  \pause 
    \item where $f$ increases, $f'$ must be positive
  \pause 
    \item where $f$ decreases, $f'$ must be negative
  \end{itemize}
\end{frame}