



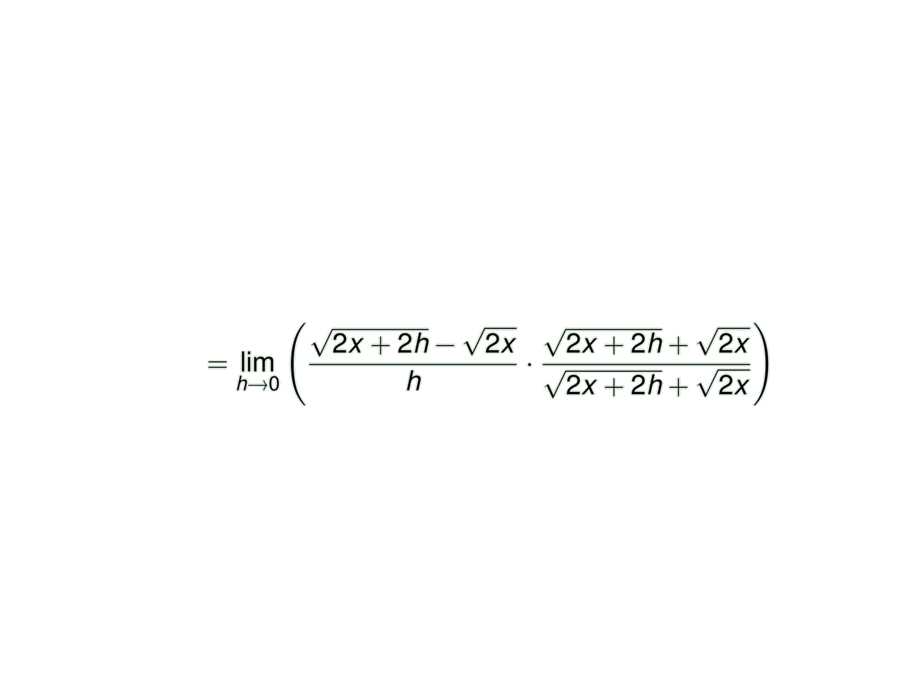































































































15/116
\begin{frame}
\frametitle{Exam Task from 2005}
\begin{exampleblock}{}
Using the definition of derivative, find $f'(x)$, where $f(x) = \sqrt{2x}$.
\pause
\begin{talign}
f'(x) &= \lim_{h\to 0} \frac{f(x+h) - f(x)}{h}\\
&\mpause[1]{= \lim_{h\to 0} \frac{\sqrt{2x+2h} - \sqrt{2x}}{h}}\\
&\mpause[2]{= \lim_{h\to 0} \left( \frac{\sqrt{2x+2h} - \sqrt{2x}}{h} \cdot \frac{\sqrt{2x+2h} + \sqrt{2x}}{\sqrt{2x+2h} + \sqrt{2x}} \right)}\\
&\mpause[3]{= \lim_{h\to 0} \left( \frac{2x+2h - 2x}{h\cdot (\;\sqrt{2x+2h} + \sqrt{2x}\;)} \right)}\\
&\mpause[4]{= \lim_{h\to 0} \left( \frac{2}{\sqrt{2x+2h} + \sqrt{2x}} \right)}\\
&\mpause[5]{= \frac{2}{2\sqrt{2x}}}
\mpause[6]{= \frac{1}{\sqrt{2x}}}
\end{talign}
\end{exampleblock}
\end{frame}

