

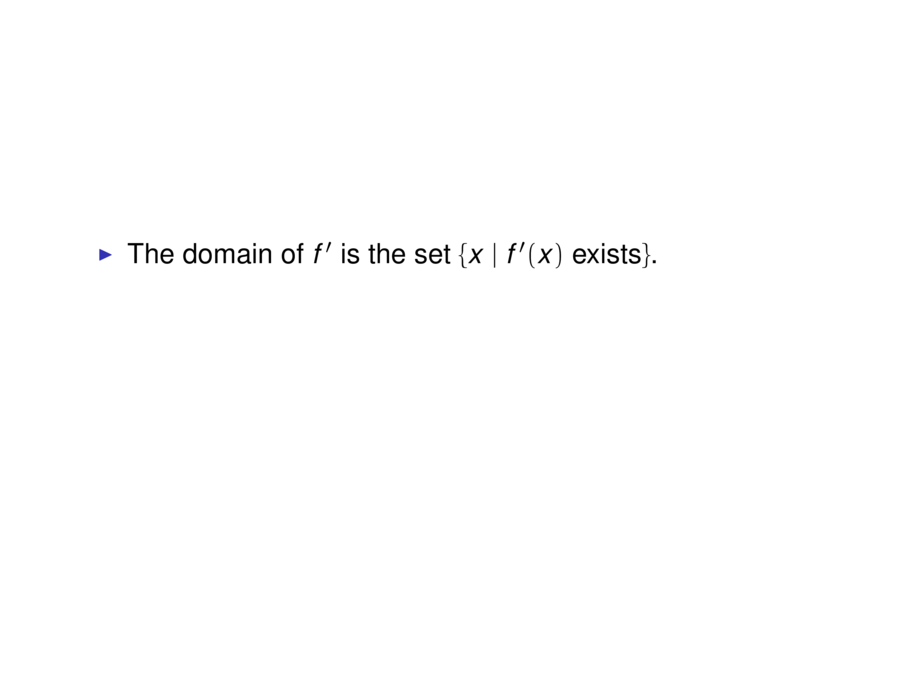

































































































9/116
\begin{frame}
\frametitle{Derivative as a Function}
\begin{block}{}
The \emph{derivative of $f$} is a function $f'$ defined by
\begin{talign}
f'(x) = \lim_{h\to 0} \frac{f(x+h) - f(x)}{h}
\end{talign}
\end{block}
\smallskip
\begin{itemize}
\pause
\item The domain of $f'$ is the set $\{x \mid f'(x) \text{ exists}\}$.
\pause\smallskip
\item Geometrically, $f'(x)$ is the slope of the tangent at $(x,f(x))$.
\end{itemize}
\pause
\begin{exampleblock}{}
Let $f(x) = x^3 - x$. Find a formula for $f'(x)$.
\pause\medskip
\begin{talign}
f'(x) &= \lim_{h\to 0} \frac{f(x+h) - f(x)}{h}
\mpause[1]{= \lim_{h\to 0} \frac{[(x+h)^3 - (x+h)] - [x^3 - x]}{h}} \\
&\mpause[2]{= \lim_{h\to 0} \frac{x^3 + 3x^2h + 3xh^2 + h^3 - x - h - x^3 + x}{h}} \\
&\mpause[3]{= \lim_{h\to 0} \frac{3x^2h + 3xh^2 + h^3 - h}{h}}
\mpause[4]{= \lim_{h\to 0} (3x^2 + 3xh + h^2 - 1)} \\
&\mpause[5]{= 3x^2 - 1}
\end{talign}
\end{exampleblock}
\end{frame}

