



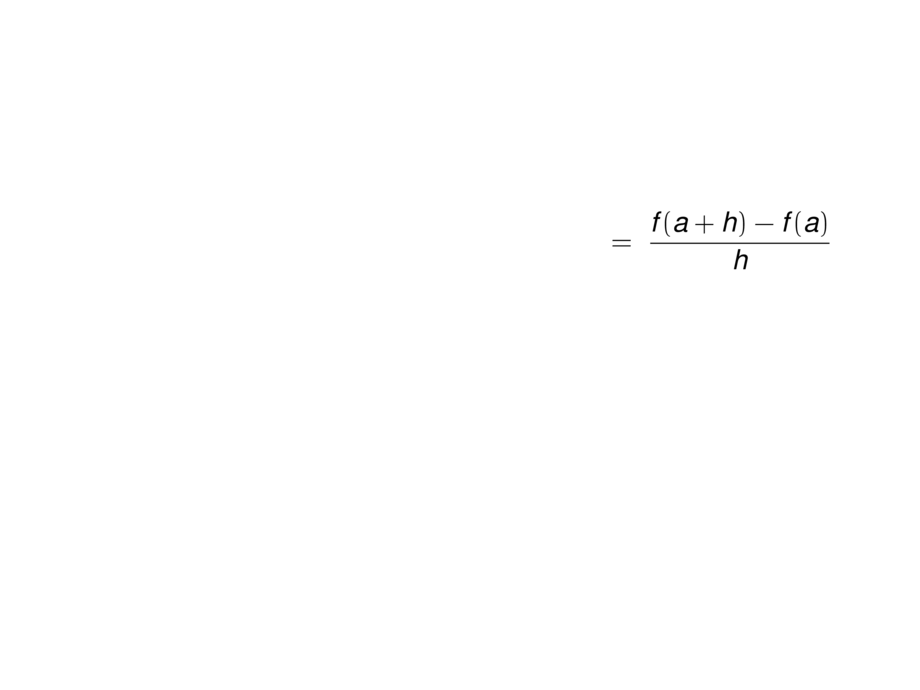
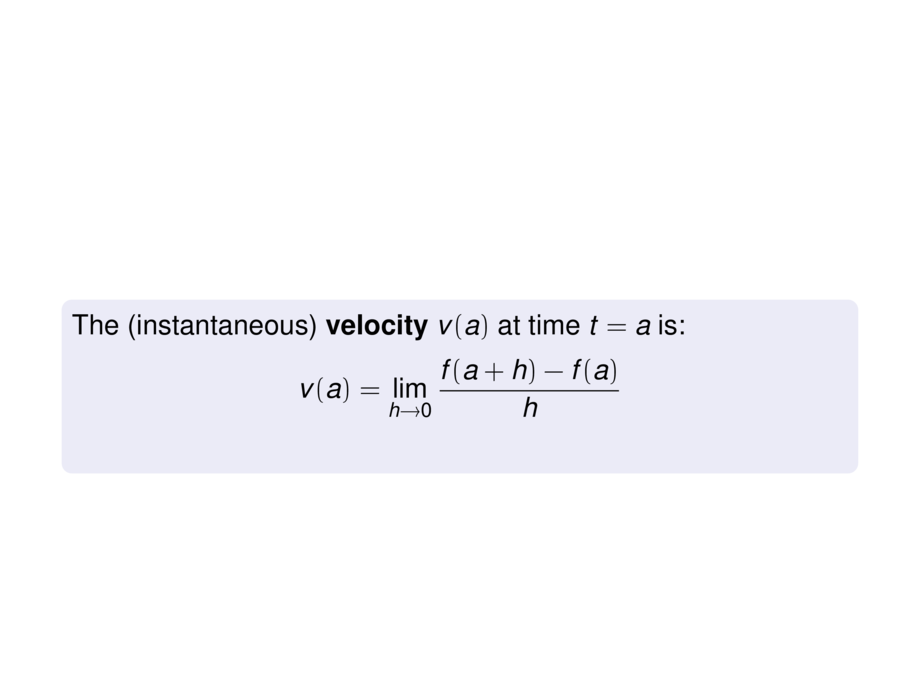


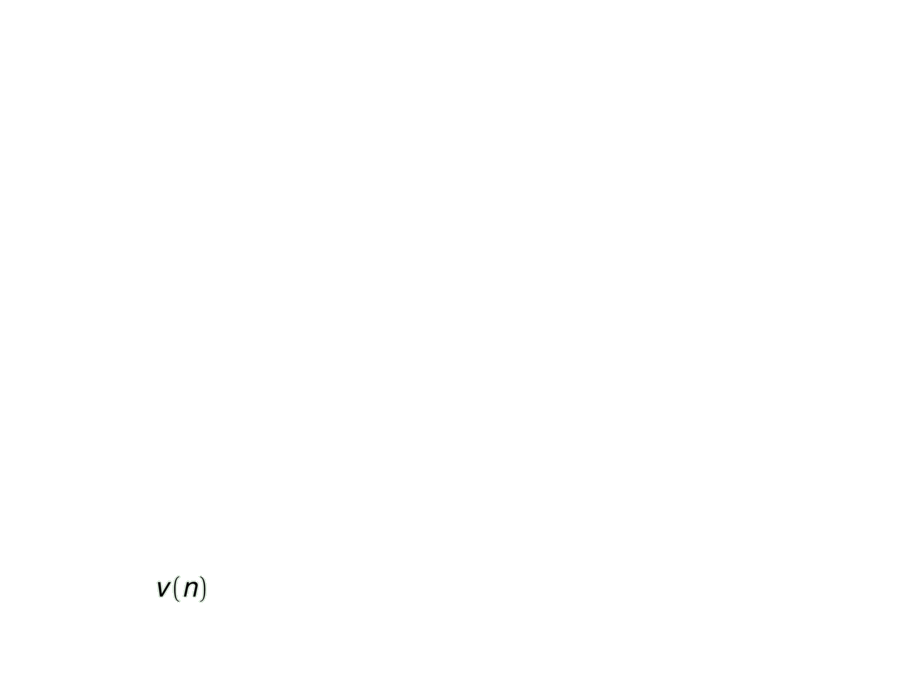



























































































36/74
\begin{frame}
\frametitle{Velocities}
Let $f(t)$ be a \emph{position function} of an object:
\begin{itemize}
\pause
\item $f(t)$ is the position (distance form the origin) after time $t$
\end{itemize}
\pause\medskip
The average velocity in the time interval $(a,a+h)$ is
\begin{talign}
\text{average velocity}
\;=\; \frac{\text{difference in position}}{\text{time difference}}
\mpause[1]{
\;=\; \frac{f(a+h) - f(a)}{h}
}
\end{talign}\vspace{-1ex}
\pause\pause
% which is the slope the line through $(a,f(a))$ and $(a+h,f(a+h))$.
% \pause
\begin{block}{}
The (instantaneous) \emph{velocity} $v(a)$ at time $t=a$ is:
\begin{talign}
v(a) = \lim_{h\to 0} \frac{f(a+h) - f(a)}{h}
\end{talign}
\pause
which is the slope of the tangent at point $(a,f(a))$.
\end{block}
\pause
\begin{exampleblock}{}
Let $f(t) = 2t^2$.
What is the speed of the object after $n$ seconds?\pause
\begin{talign}
v(n)
&\mpause[1]{= \lim_{h\to 0} \frac{2\cdot (n+h)^2 - 2\cdot n^2}{h}}
\mpause[2]{= \lim_{h\to 0} \frac{4nh+2\cdot h^2}{h}}\\
&\mpause[3]{= \lim_{h\to 0} (4n+2\cdot h)}
\mpause[4]{= 4n}
\end{talign}
\end{exampleblock}
\vspace{15cm}
\end{frame}

