\begin{frame}
  \frametitle{Finding a Tangent}
  
  Alternative definition of the slope:
  \begin{block}{}
    The slope of $f$ at point $(a,f(a))$ is:
    \begin{talign}
      m = \lim_{h\to 0} \frac{f(a+h) - f(a)}{h}
    \end{talign}
  \end{block}
  \pause
  \begin{block}{}
    The slope $m$ is also called the \emph{slope of the curve} at the point. 
  \end{block}
  \pause\medskip

  \begin{exampleblock}{}
    Find an equation of the tangent to $f(x) = \frac{3}{x}$ at point $(3,1)$.
    \pause\medskip
    
    The slope is:
    \begin{talign}
      m &= \lim_{h\to 0} \frac{f(3+h) - f(3)}{h}
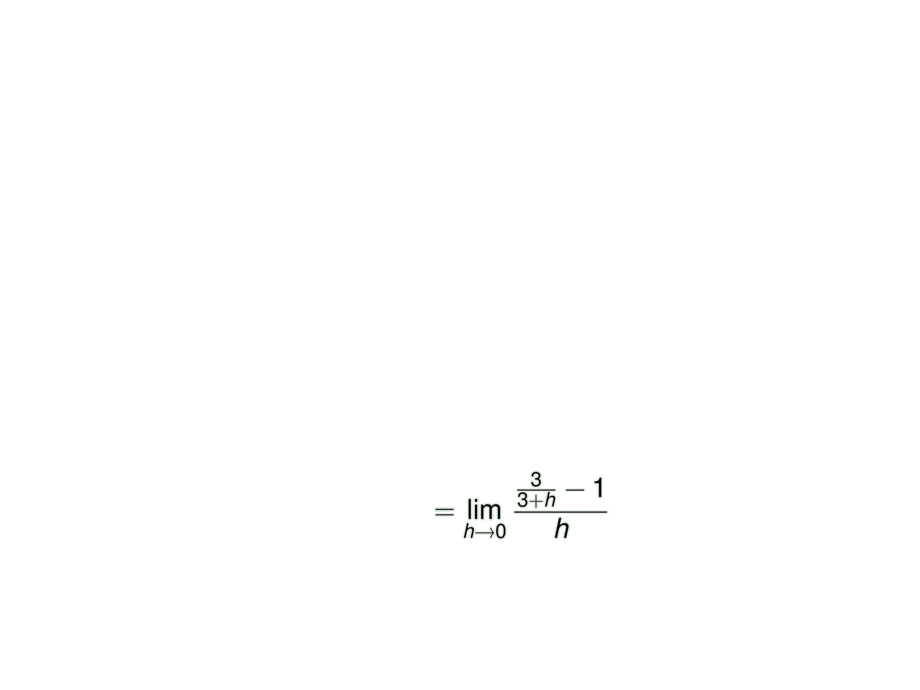
      \mpause[1]{= \lim_{h\to 0} \frac{\frac{3}{3+h} - 1}{h}}
      \mpause[2]{= \lim_{h\to 0} \frac{\frac{3 - (3+h)}{3+h}}{h}}\\
      &\mpause[3]{= \lim_{h\to 0} \frac{-h}{h(3+h)}}
      \mpause[4]{= \lim_{h\to 0} -\frac{1}{3+h}}
      \mpause[5]{= -\frac{1}{3}}
    \end{talign}
    \pause[10]
    Thus $y - 1 = -\frac{1}{3} (x-3)$\pause, that is, the tangent is $y = 2 - \frac{x}{3}$. 
  \end{exampleblock}
\end{frame}