


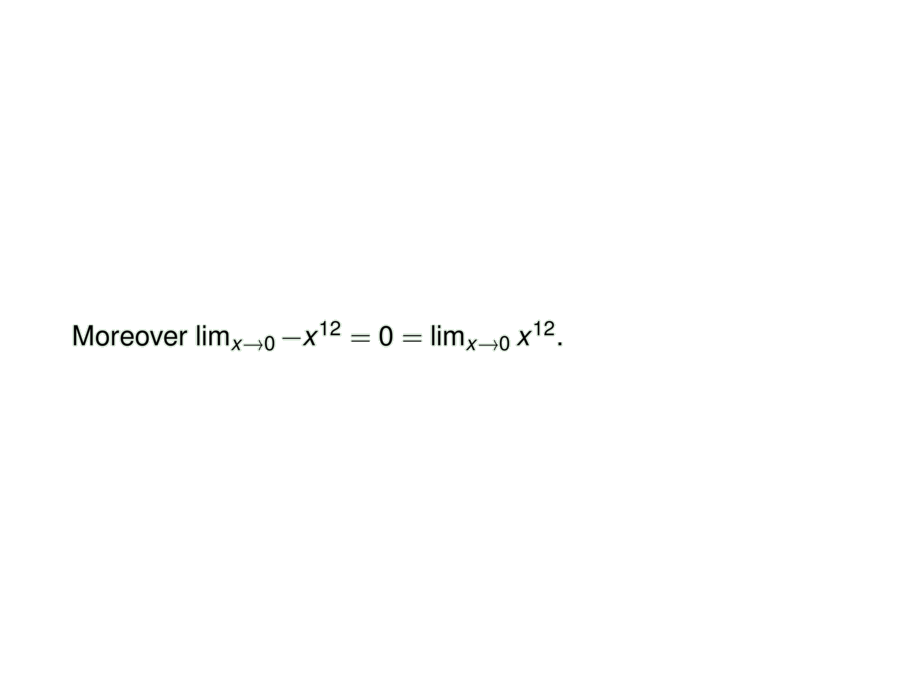
































































































52/65
\begin{frame}
\frametitle{1st Midterm Exam - Review}
\begin{exampleblock}{}
Prove $\lim_{x \to 0} g(x) = 0$ where $g(x) = x^{12} \cdot \cos \left( \frac{1+e^{50x}}{13.2 x^2} \right)$.
\pause\medskip
We know that the range of $\cos$ is $[-1,1]$. Thus
\begin{talign}
-x^{12} \le g(x) \le x^{12}
\end{talign}
\pause
Moreover $\lim_{x\to 0} -x^{12} = 0 = \lim_{x\to 0} x^{12}$.
\pause\medskip
Thus we can apply the Squeeze Theorem with
\begin{itemize}
\item lower bound $-x^{12}$ (i.e. $\le g(x)$), and
\item upper bound $x^{12}$ (i.e. $\ge g(x)$)
\end{itemize}
and it follows that
\begin{talign}
\lim_{x\to 0} g(x) = 0
\end{talign}
\end{exampleblock}
\end{frame}

