

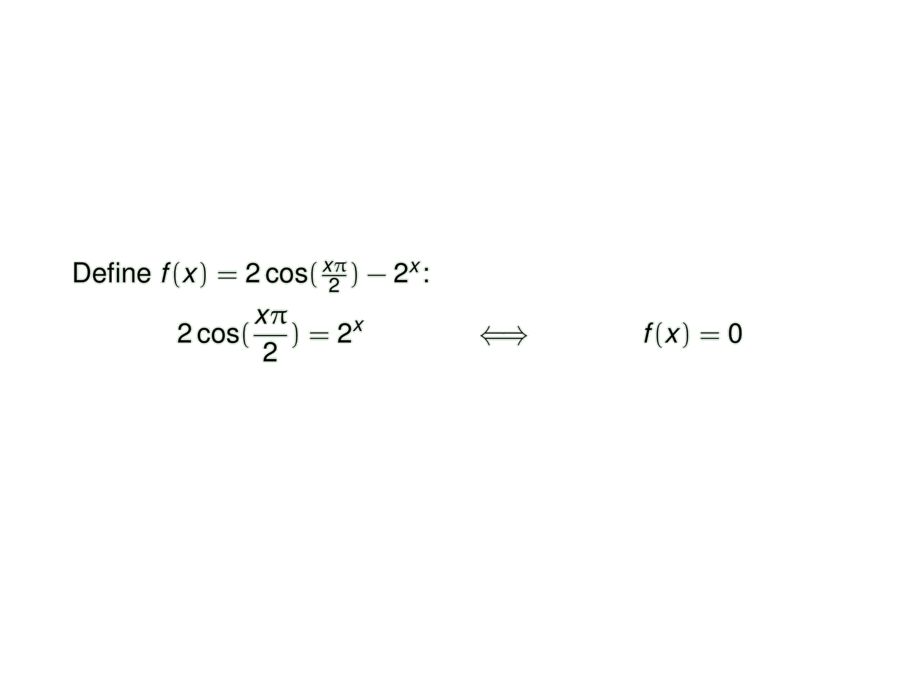






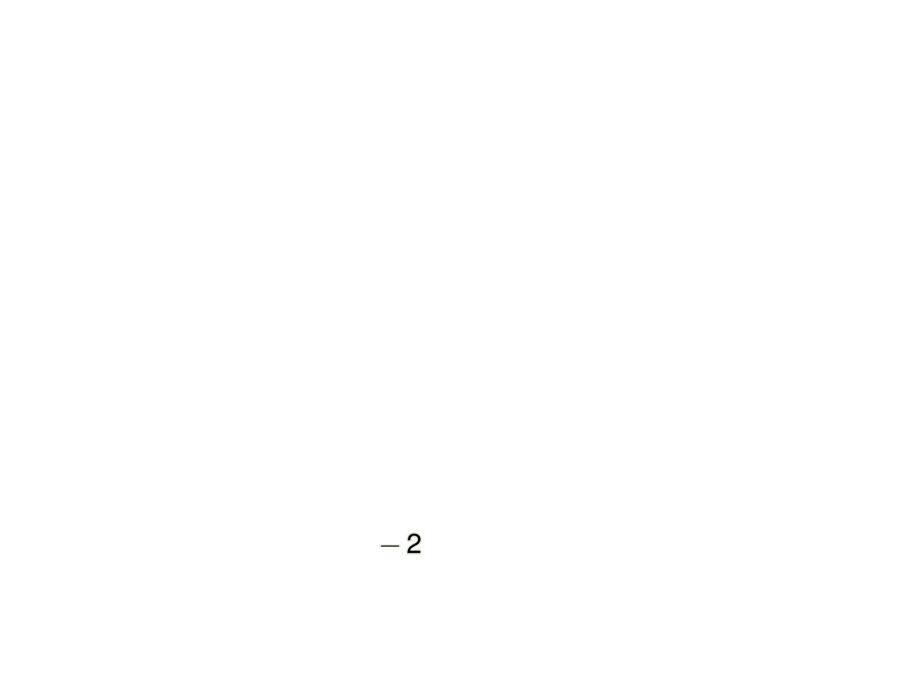


























































































46/65
\begin{frame}
\frametitle{1st Midterm Exam - Review}
\begin{exampleblock}{}
Prove that the equation
\begin{talign}
2\cos(\frac{x\pi}{2}) = 2^x
\end{talign}
has a solution for $x$ on the interval $[0,1]$.
\pause\medskip
Define $f(x) = 2\cos(\frac{x\pi}{2}) - 2^x$:
\begin{talign}
2\cos(\frac{x\pi}{2}) = 2^x &&\iff&&
f(x) = 0
\end{talign}
\pause
We have:
\begin{itemize}
\pause
\item $f(x)$ is defined on $[0,1]$
\pause
\item $f(x)$ is continuous on its domain since it is a composition,
product, division and multiplication of continuous functions
\pause
\item $f(0) = \pause 1$ \pause and $f(1) = \pause -2$
\end{itemize}
\pause
Since $0$ is between $-2$ and $1$, by the Intermediate Value Theorem, \pause
there exists $c$ in $(0,1)$ such that $f(c) = 0$. \pause
This $c$ is a solution of the equation.
\end{exampleblock}
\end{frame}

