




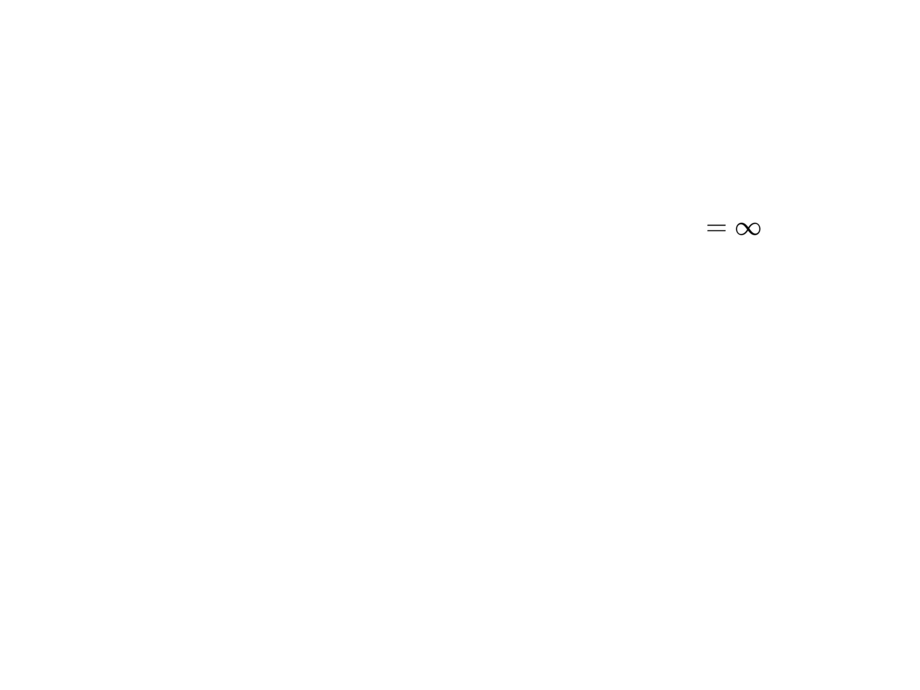
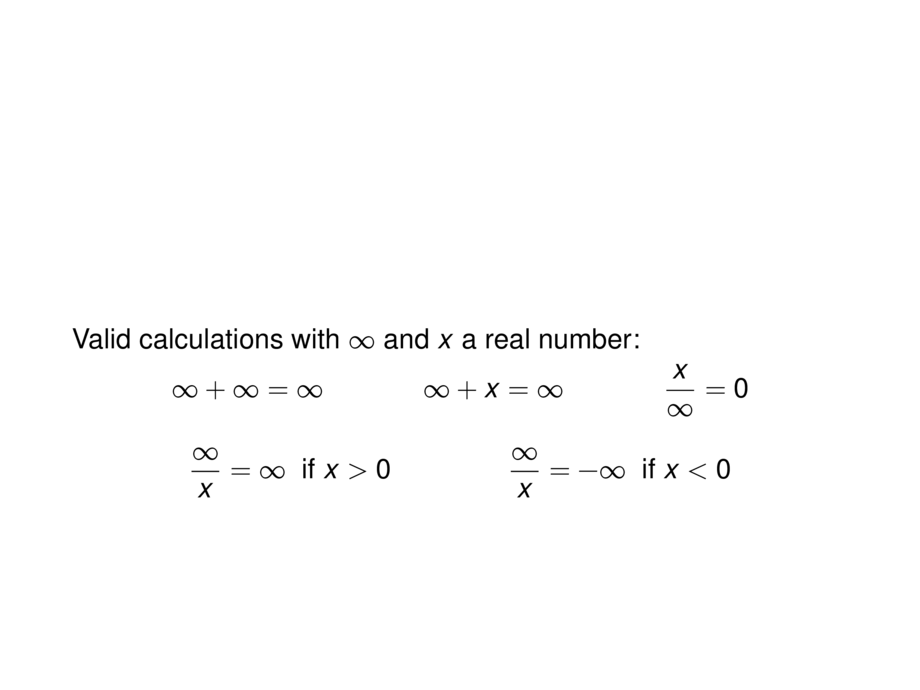





























































































111/119
\begin{frame}
\frametitle{Infinite Limits at Infinity: Heuristics}
\alert{All on this slide is heuristics, not laws!}
\pause\bigskip
On the last slide we could have reasoned as follows:
\begin{talign}
\lim_{x\to\infty} (x^2 - x)
\mpause[1]{= \lim_{x\to\infty} x \cdot \lim_{x\to\infty} (x - 1) }
\mpause[2]{= \infty \cdot \infty}
\mpause[3]{= \infty}
\end{talign}
\pause\pause\pause\pause\bigskip
Valid calculations with $\infty$ and $x$ a real number:
\begin{talign}
\infty + \infty = \infty &&
\infty + x = \infty &&
\frac{x}{\infty} = 0
\end{talign}
\begin{talign}
\frac{\infty}{x} = \infty \text{\;\;if $x > 0$} &&
\frac{\infty}{x} = -\infty \text{\;\;if $x < 0$}
\end{talign}
\pause\smallskip
\alert{Invalid, undefined expressions}:
\begin{talign}
\infty - \infty &&
\infty + (-\infty) &&
\frac{\infty}{\infty} &&
0 \cdot \infty
\end{talign}
\end{frame}

