


































































































8/119
\begin{frame}
\frametitle{Limits at Infinity: Horizontal Asymptotes}
\begin{block}{}
The line $y = L$ is called \emph{horizontal asymptote}
of a function $f$ if
\begin{talign}
\lim_{x\to\infty} f(x) = L &&\text{or} &&\lim_{x\to-\infty} f(x) = L
\end{talign}
\end{block}
\pause\bigskip
\only<2>{
\begin{exampleblock}{}
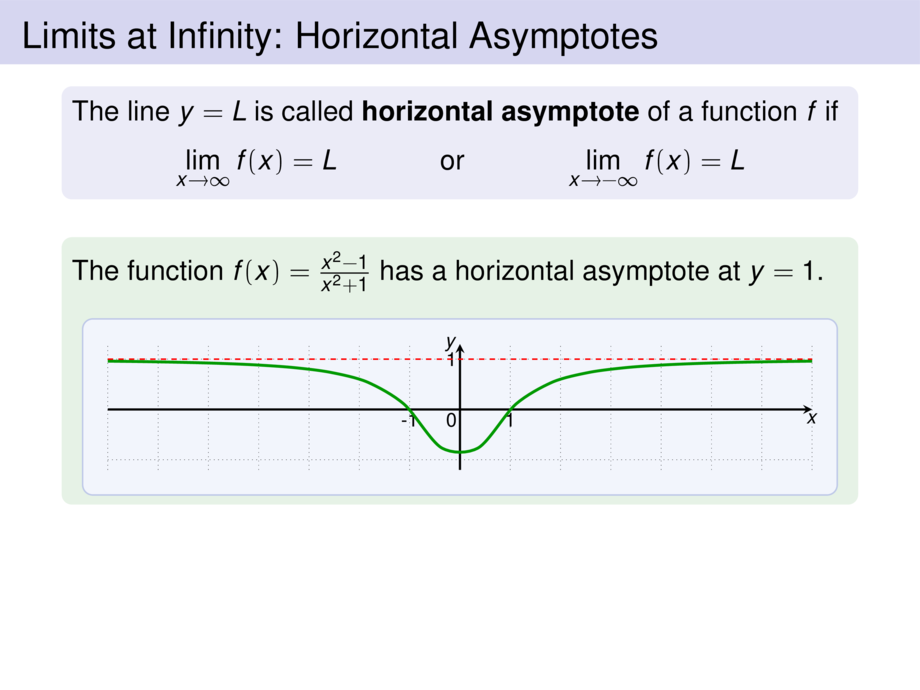
The function $f(x) = \frac{x^2 - 1}{x^2 + 1}$ has a horizontal asymptote at $y = 1$.
\begin{center}
\scalebox{.7}{
\begin{tikzpicture}[default]
\diagram{-7}{7}{-1.2}{1.3}{1}
\diagramannotatez
\diagramannotatex{-1,1}
\diagramannotatey{1}
\draw[cgreen,ultra thick] plot[smooth,domain=-7:7,samples=20] function{(x**2 - 1)/(x**2 + 1)};
\onslide<2->{
\draw[cred,dashed] (-7,1) -- (7,1);
}
\end{tikzpicture}
}
\end{center}
\end{exampleblock}
}
\only<3>{
\begin{exampleblock}{}
The inverse tangent $\tan^{-1}$ has horizontal asymptotes
\begin{talign}
y = -\frac{\pi}{2} && \text{and} && y = \frac{\pi}{2}
\end{talign}
\begin{center}
\scalebox{.7}{
\begin{tikzpicture}[default,yscale=.8]
\diagram{-7}{7}{-2}{2}{1}
\diagramannotatez
\diagramannotatexx{-pi/$-\pi$,pi/$\pi$}
\diagramannotateyy{{-0.5*pi}/$-\frac{\pi}{2}$,{0.5*pi}/$\frac{\pi}{2}$}
\draw[cgreen,ultra thick] plot[smooth,domain=-7:7,samples=50] function{atan(x)};
\onslide<2->{
\draw[cred,dashed] (-7,-0.5*pi) -- (7,-0.5*pi);
\draw[cred,dashed] (-7,0.5*pi) -- (7,0.5*pi);
}
\end{tikzpicture}
}
\end{center}\vspace{-1ex}
\pause
\begin{talign}
\lim_{x\to -\infty} \tan^{-1}{x} = -\frac{\pi}{2} && \lim_{x\to \infty} \tan^{-1}{x} = \frac{\pi}{2}
\end{talign}
\end{exampleblock}
}
\vspace{10cm}
\end{frame}

