


































































































4/119
\begin{frame}
\frametitle{Limits at Infinity}
Lets investigate the behavior of the function
\begin{talign}
f(x) = \frac{x^2 - 1}{x^2 + 1}
\end{talign}
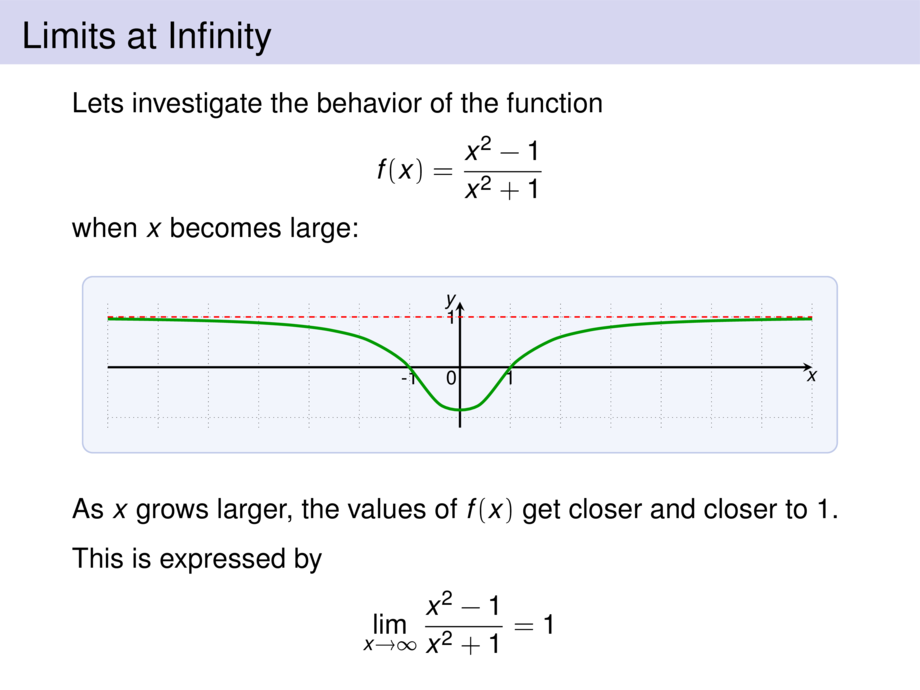
when $x$ becomes large:
\begin{center}
\scalebox{.7}{
\begin{tikzpicture}[default]
\diagram{-7}{7}{-1.2}{1.3}{1}
\diagramannotatez
\diagramannotatex{-1,1}
\diagramannotatey{1}
\draw[cgreen,ultra thick] plot[smooth,domain=-7:7,samples=20] function{(x**2 - 1)/(x**2 + 1)};
\onslide<2->{
\draw[cred,dashed] (-7,1) -- (7,1);
}
\end{tikzpicture}
}
\end{center}
\pause
As $x$ grows larger, the values of $f(x)$ get closer and closer to $1$.\\
\pause\medskip
This is expressed by
\begin{talign}
\lim_{x\to\infty} \frac{x^2 - 1}{x^2 + 1} = 1
\end{talign}
\end{frame}

