\begin{frame}
  \frametitle{Continuity: Intermediate Value Theorem}

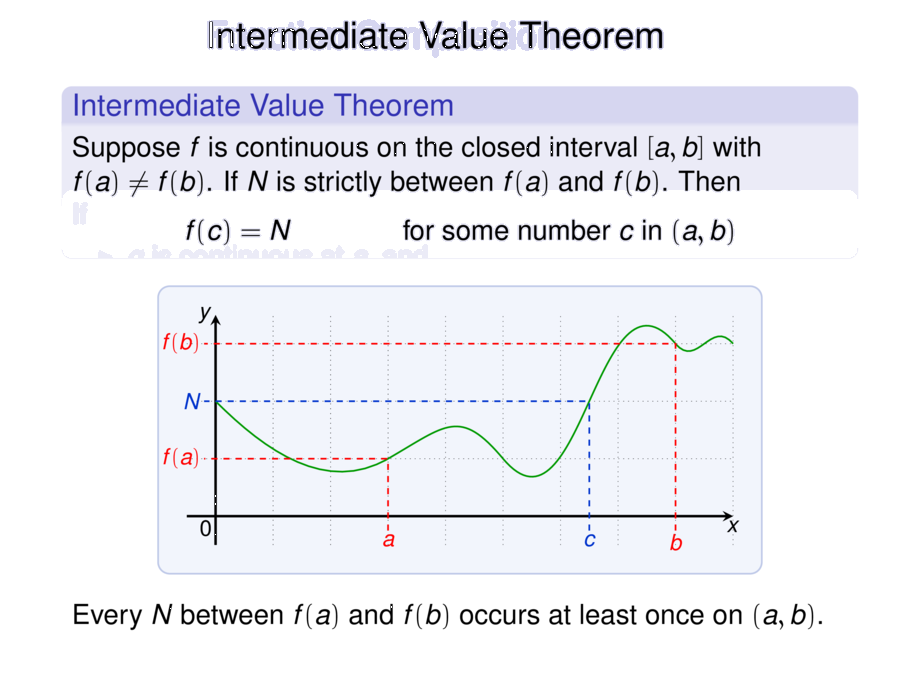
  \begin{block}{Intermediate Value Theorem}
    Suppose $f$ is continuous on the closed interval $[a,b]$
    with $f(a) \ne f(b)$.
    If $N$ is strictly between $f(a)$ and $f(b)$.
    Then 
    \begin{talign}
      f(c) = N &&\text{for some number $c$ in $(a,b)$}
    \end{talign}
  \end{block}  
  \vspace{-2ex}
  
  \begin{center}
    \scalebox{.8}{
    \begin{tikzpicture}[default]
      \diagram{-.5}{9}{-.5}{3.5}{1}
      \diagramannotatez
%       \diagramannotatex{1,2,3,4,5,6,7,8}
%       \diagramannotatey{1,2}
      \draw[cgreen] (0,2) to[out=-45,in=-150] (3,1);
      \draw[cgreen] (3,1) to[out=30,in=130,looseness=1.5] (5,1);
      \draw[cgreen] (5,1) to[out=-50,in=130,looseness=1.5] (8,3);
      \draw[cgreen] (8,3) to[out=-50,in=130,looseness=1.5] (9,3);

      \draw[cred,dashed] (3,-.25) -- node[at start,below] {$a$} (3,1) -- node[at end,left] {$f(a)$} (-0.2,1);
      \draw[cred,dashed] (8,-.25) -- node[at start,below] {$b$} (8,3) -- node[at end,left] {$f(b)$} (-0.2,3);
      \draw[cblue,dashed] (6.5,-.25) -- node[at start,below] {$c$} (6.5,2) -- node[at end,left] {$N$} (-0.2,2);
    \end{tikzpicture}
    }
  \end{center}
  
  Every $N$ between $f(a)$ and $f(b)$ occurs at least once on $(a,b)$.\\\pause
  Intuitively: the graph cannot jump over the line $y= N$.
  \bigskip
\end{frame}