

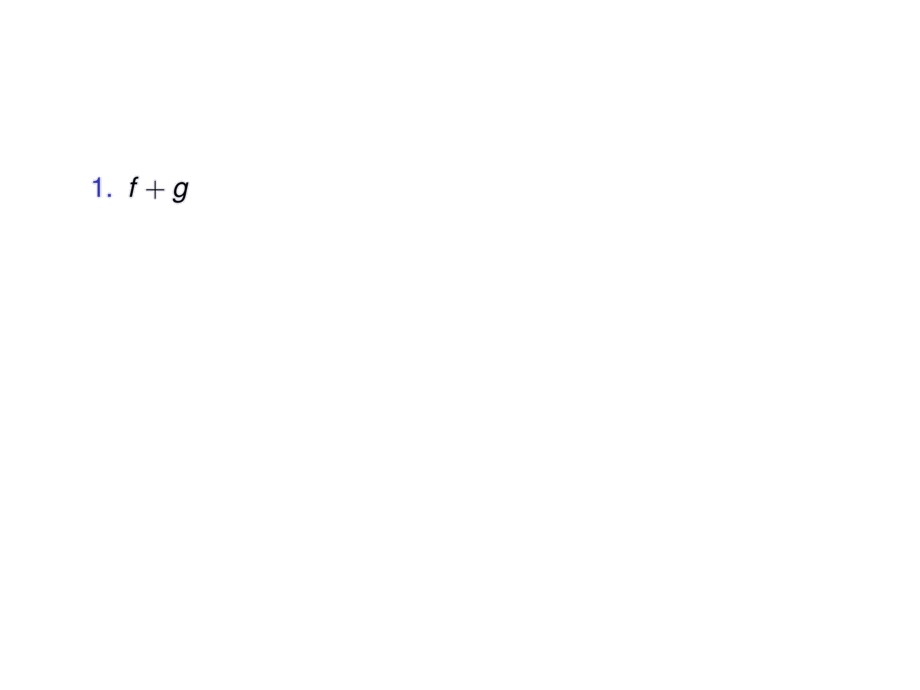
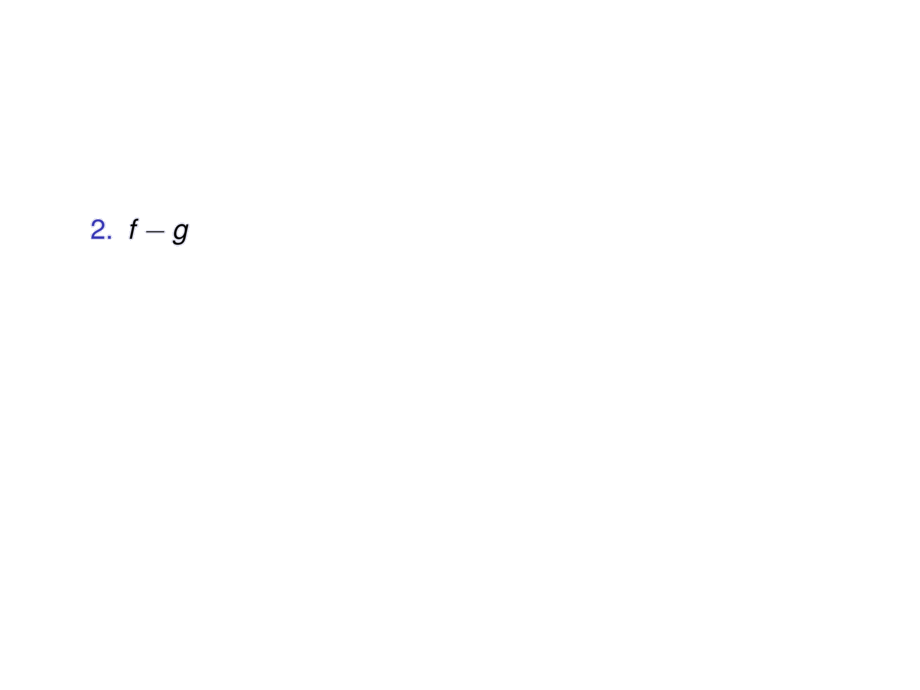
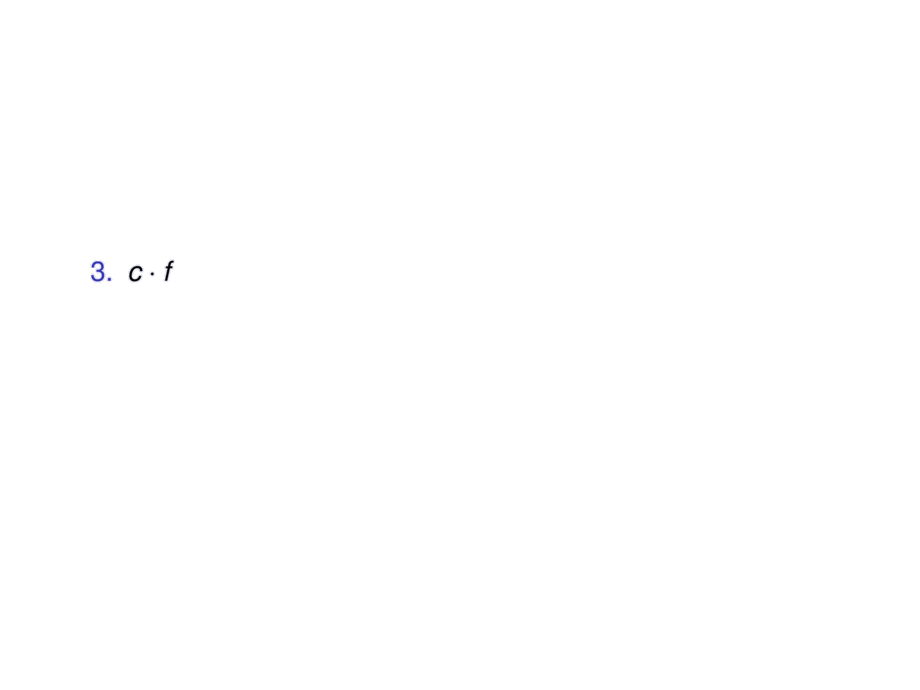
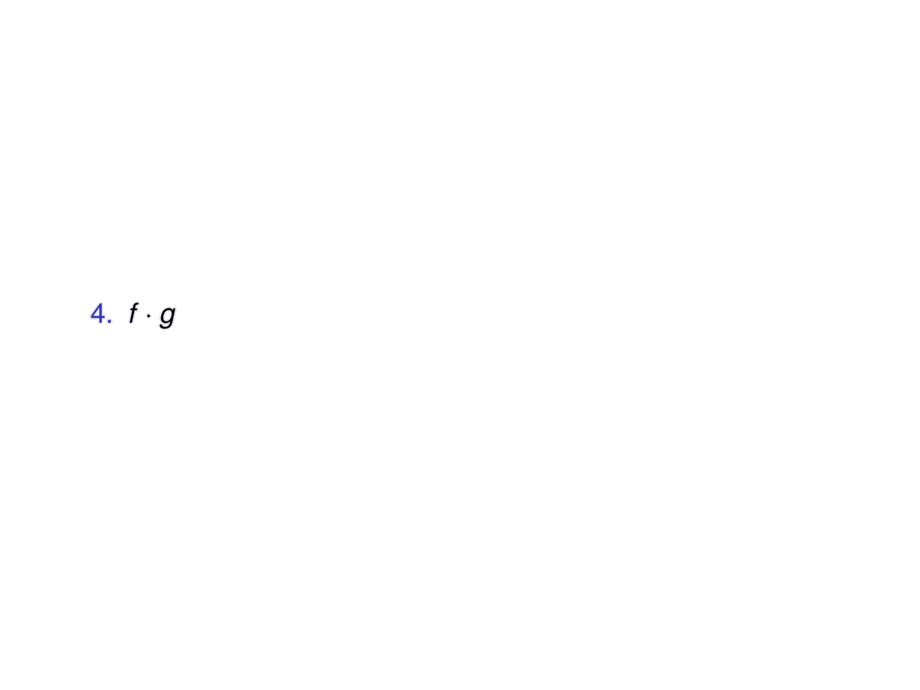
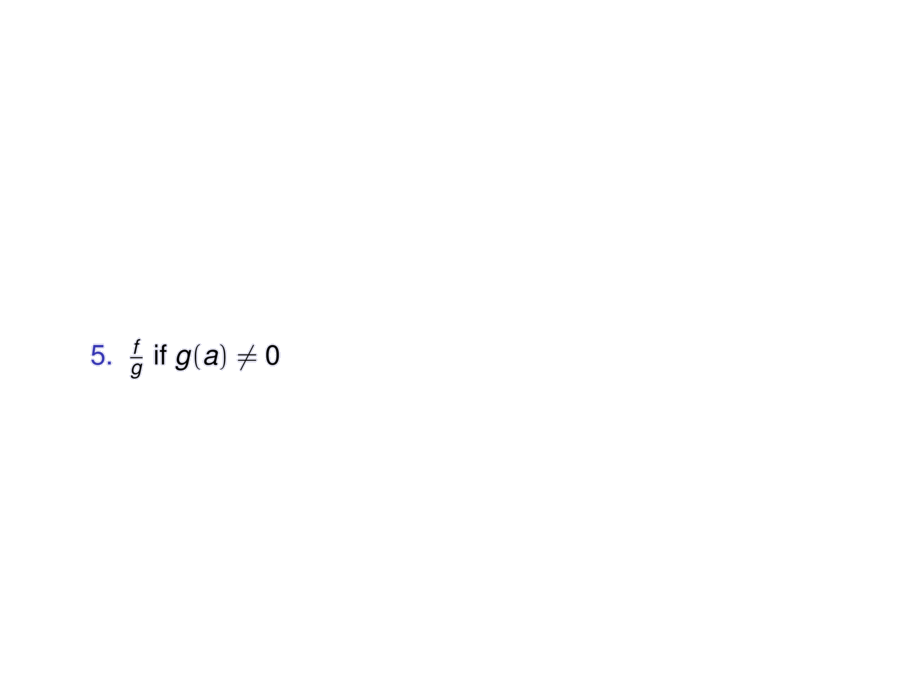



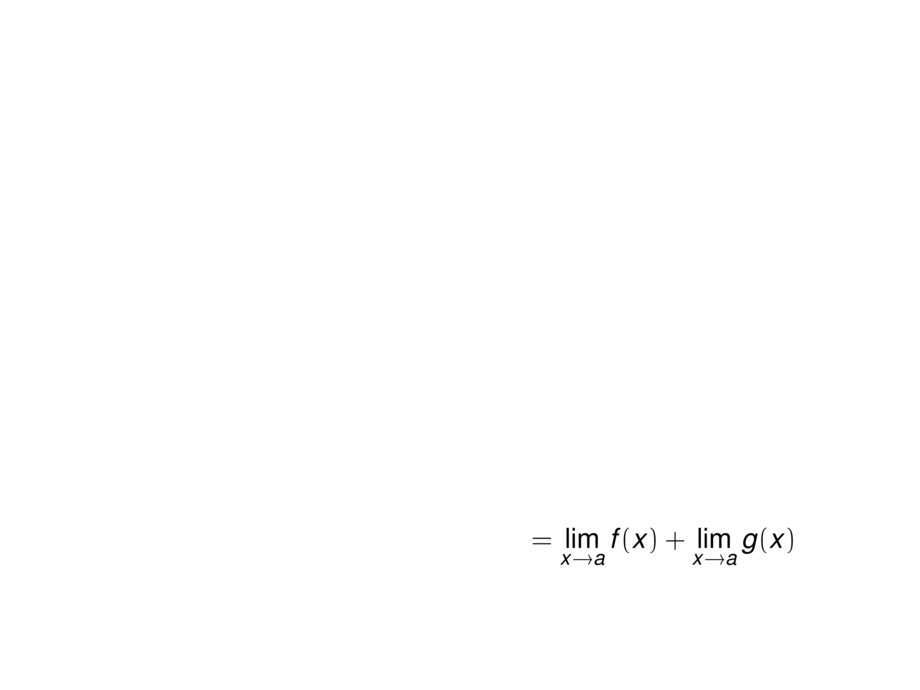
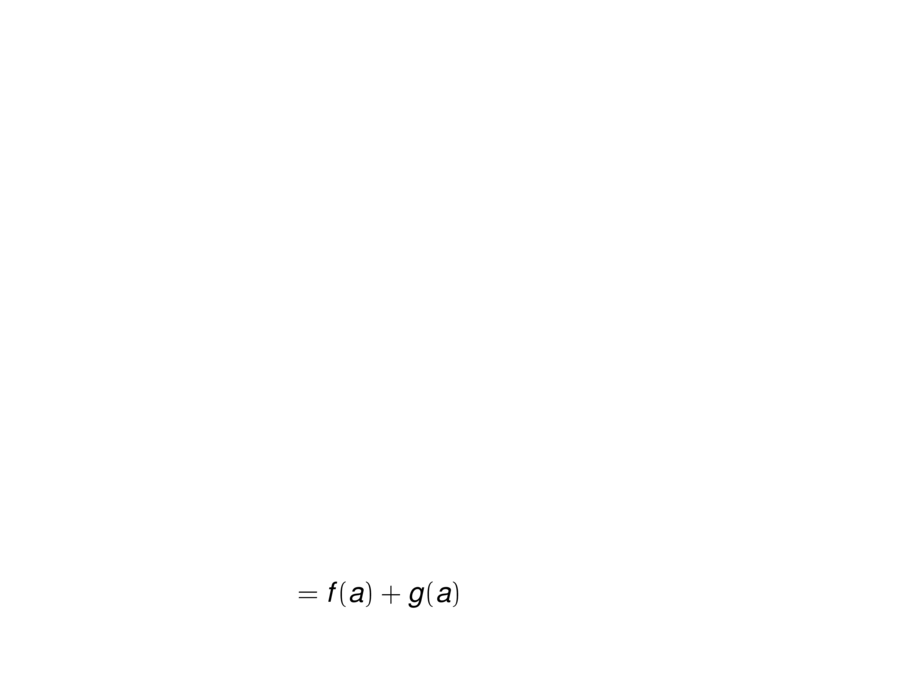
























































































48/98
\begin{frame}
\frametitle{Continuity: Composition of Functions}
\begin{block}{}
If $f$ and $g$ are continuous at $a$ and $c$ is a constant,
then the following functions are continuous at $a$:
\begin{enumerate}
\pause
\item $f+g$
\pause
\item $f-g$
\pause
\item $c\cdot f$
\pause
\item $f\cdot g$
\pause
\item $\frac{f}{g}$ if $g(a) \ne 0$
\end{enumerate}
\end{block}
\pause\bigskip
All of these can be proven from the limit laws!
\pause\bigskip
For example, (1) can be proven as follows:
\begin{talign}
\lim_{x\to a}(f+g)(x)
&\mpause[1]{= \lim_{x\to a}[f(x) + g(x)]}
\mpause[2]{= \lim_{x\to a} f(x) + \lim_{x\to a} g(x)}\\
&\mpause[3]{= f(a) + g(a)}
\mpause[4]{= (f+g)(a)}
\end{talign}
\pause\pause\pause\pause\pause
Thus $f+g$ is continuous at $a$.
\vspace{10cm}
\end{frame}

