







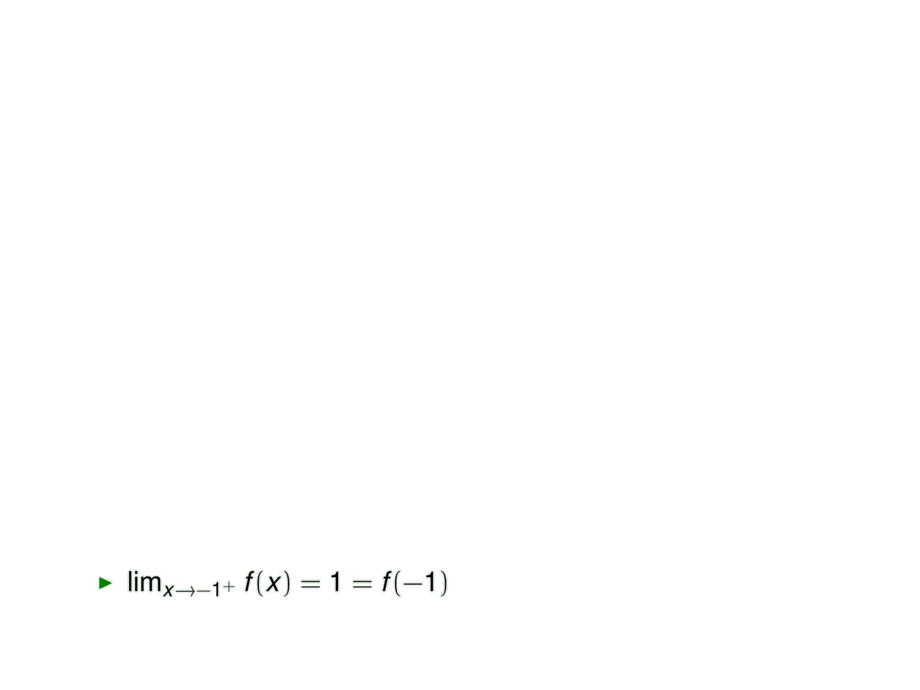
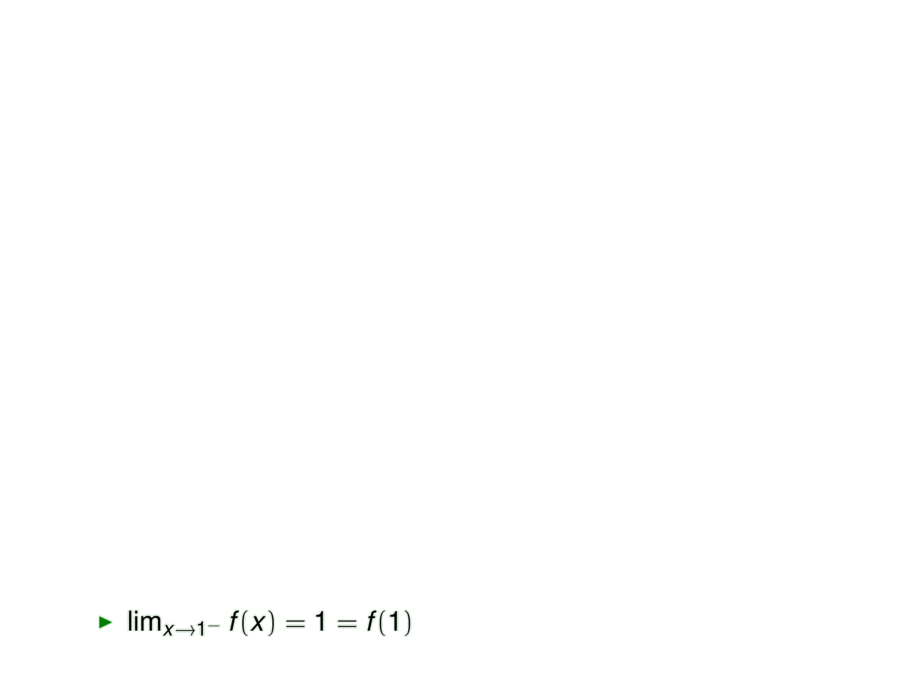


























































































36/98
\begin{frame}
\frametitle{Continuity on Intervals}
\begin{block}{}
A function $f$ is \emph{continuous} on an interval if
it is continuous on every number in the interval.
\end{block}
\pause\medskip
If the interval is left- and/or right-closed, then
\begin{itemize}
\item At the left-end we are only interested in right-continuity.
\item At the right-end we are only interested in left-continuity.
\end{itemize}
(the values outside of the interval do not matter)
\pause
\begin{exampleblock}{}
Show that $f(x) = 1 - \sqrt{1-x^2}$ is continuous on $[-1,1]$.
\pause\medskip
For $-1 < a < 1$ we have by the limit laws:
\begin{talign}
\lim_{x\to a} f(x)
% = 1 - \lim_{x\to a} \sqrt{1-x^2}
\mpause[1]{ = 1 - \sqrt{\lim_{x\to a}(1-x^2)} }
\mpause[2]{ = 1 - \sqrt{1-a^2} = f(a) }
\end{talign}
\pause\pause\pause
Similar calculations show
\begin{itemize}
\pause
\item
$\lim_{x\to -1^+} f(x) = 1 = f(-1)$
\pause
\item
$\lim_{x\to 1^-} f(x) = 1 = f(1)$
\end{itemize}
\pause
Therefore $f$ is continuous on $[-1,1]$.
\end{exampleblock}
\end{frame}

