\begin{frame}
  \frametitle{Continuity: Examples}

  \begin{center}
    \scalebox{.8}{
    \begin{tikzpicture}[default]
      \diagram{-.5}{9}{-.5}{3.2}{1}
      \diagramannotatez
      \diagramannotatex{1,2,3,4,5,6,7,8}
      \diagramannotatey{1,2}
      \draw[cred] (-.5,0) to[out=51,in=180] (3,3);
      \draw[cred] (3,2) to[out=-45,in=180] (5,1);
      \draw[cred] (5,1) to[out=0,in=150] (9,3);
      
      \node[exclude={cred}] at (1,2) {};
      \node[include={cred}] at (3,2) {};
      \node[exclude={cred}] at (3,3) {};
      \node[exclude={cred}] at (5,1) {};
      \node[include={cred}] at (5,2.5) {};
    \end{tikzpicture}
    }
  \end{center}
  
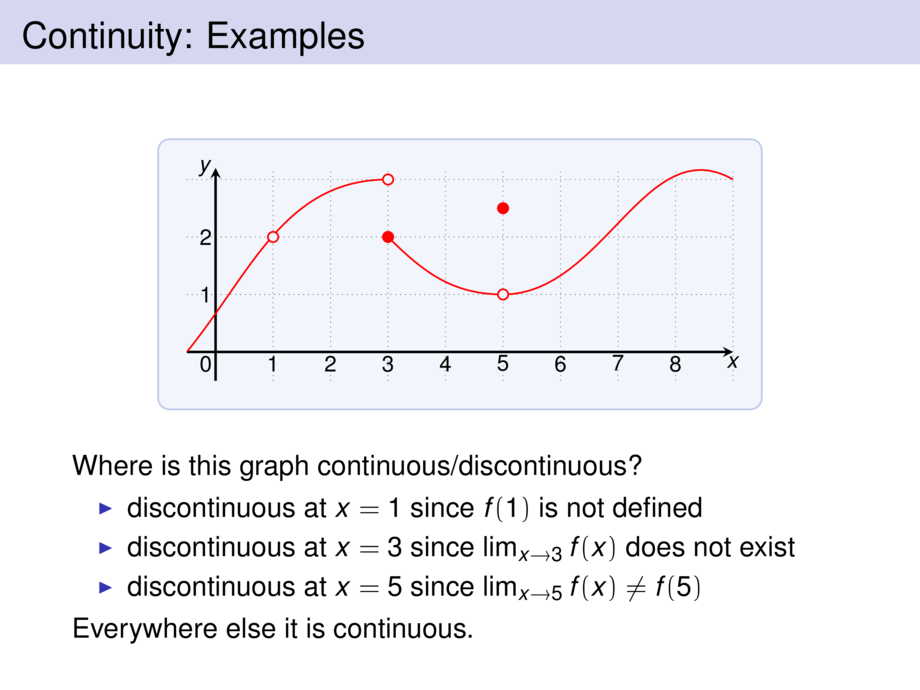
  Where is this graph continuous/discontinuous?
  \begin{itemize}
  \pause
    \item discontinuous at $x = 1$ since $f(1)$ is not defined
  \pause
    \item discontinuous at $x = 3$ since $\lim_{x\to 3} f(x)$ does not exist
  \pause
    \item discontinuous at $x = 5$ since $\lim_{x\to 5} f(x) \ne f(5)$
  \end{itemize}
  \pause
  Everywhere else it is continuous.
\end{frame}