
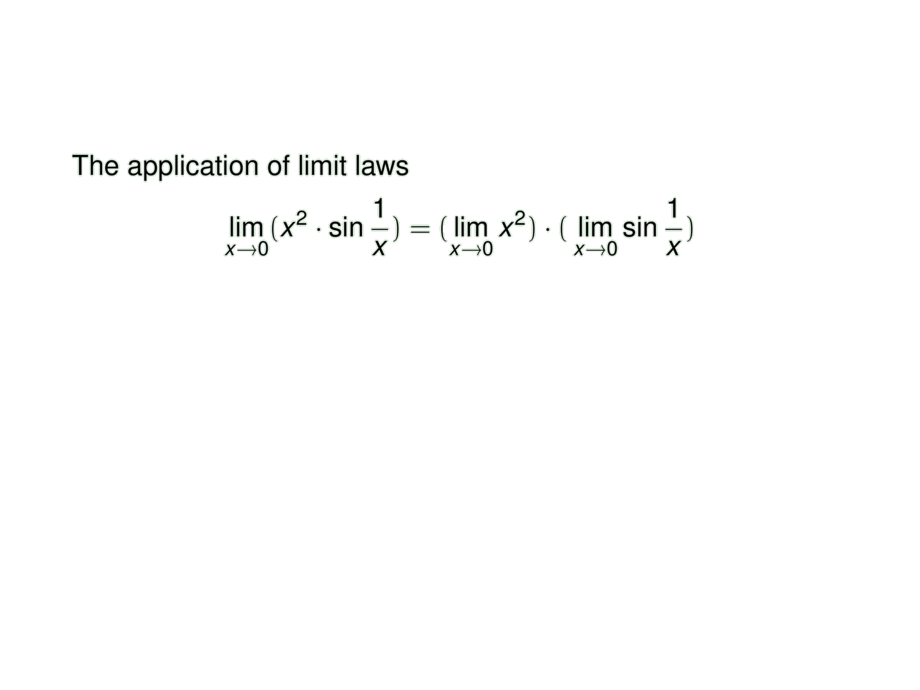

































































































133/145
\begin{frame}
\frametitle{Properties of Limits}
\begin{exampleblock}{}
Show that $\lim_{x \to 0} g(x) = 0$ where $g(x) = x^2 \cdot \sin \frac{1}{x}$.
\pause\medskip
The application of limit laws
\begin{talign}
\lim_{x \to 0} ( x^2 \cdot \sin \frac{1}{x} ) = (\lim_{x \to 0} x^2) \cdot (\alert<3->{\lim_{x \to 0} \sin \frac{1}{x}})
\end{talign}\pause
does not work since $\lim_{x \to 0} \sin \frac{1}{x}$ does not exist.
\pause\bigskip
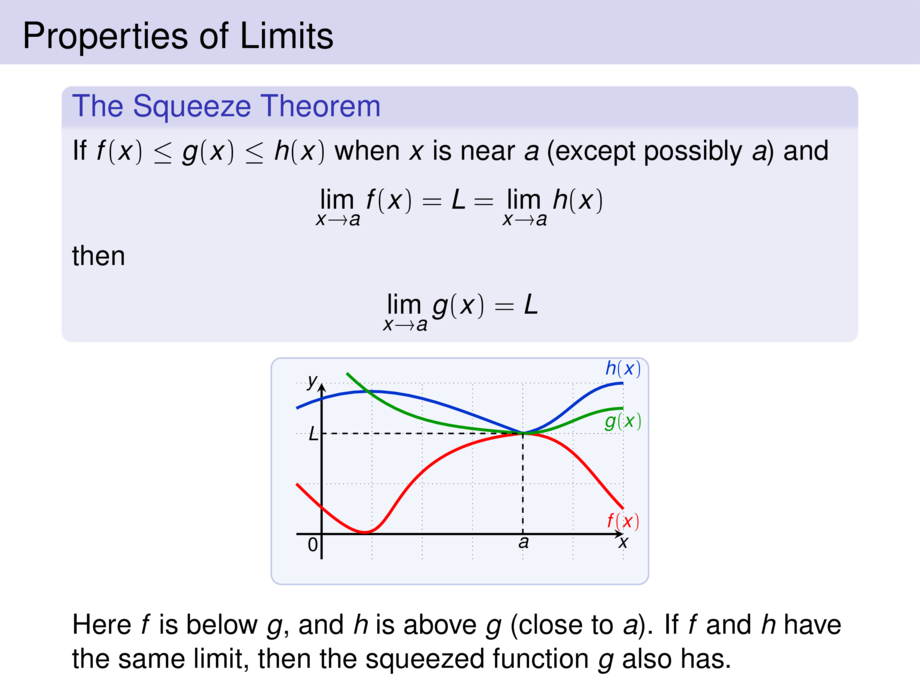
To apply the squeeze theorem we need:
\begin{itemize}
\pause
\item a function $f$ smaller ($\le$) than $g$, and
\pause
\item a function $h$ bigger ($\ge$) than $g$
\end{itemize}
\pause
for which $\lim_{x\to 0} f(x) = 0$ and $\lim_{x\to 0} h(x) = 0$.
\pause\bigskip
We know that $-1 \le \sin \frac{1}{x} \le 1$ \pause
and hence% (we multiply everything with the non-negative $x^2$)
\begin{talign}
-x^2 \quad\le\quad x^2 \cdot \sin \frac{1}{x} \quad\le\quad x^2
\end{talign}
\end{exampleblock}
\vspace{10cm}
\end{frame}

