\begin{frame}
  \frametitle{Properties of Limits}
  \begin{block}{The Squeeze Theorem}
    If $f(x) \le g(x) \le h(x)$ when $x$ is near $a$ (except possibly $a$)
    and
    \begin{talign}
      \lim_{x\to a} f(x) = L = \lim_{x\to a} h(x)
    \end{talign}
    then
    \begin{talign}
      \lim_{x\to a} g(x) = L
    \end{talign}
  \end{block}
  \begin{center}
    \scalebox{.7}{
    \begin{tikzpicture}[default]
      \diagram{-.5}{6}{-.5}{3}{1}
      \diagramannotatez
      \draw[cred,ultra thick] (-.5,1) to[out=-45,in=185,looseness=2] (4,2) to[out=0,in=135,looseness=1] node [at end,below] {$f(x)$} (6,.5);
      \draw[cblue,ultra thick] (-.5,2.5) to[out=25,in=160,looseness=1] (4,2) to[out=10,in=180,looseness=1] node [at end,above] {$h(x)$} (6,3);
      \draw[cgreen,ultra thick] (0.5,3.2) to[out=-45,in=175,looseness=1] (4,2) to[out=0,in=180,looseness=1] node [at end,below] {$g(x)$} (6,2.5);
      \draw[dashed] (4,0) -- node[at start,below] {$a$} (4,2) -- node[at end,left] {$L$} (0,2);
    \end{tikzpicture}
    }
  \end{center}
  \pause\vspace{-2ex}
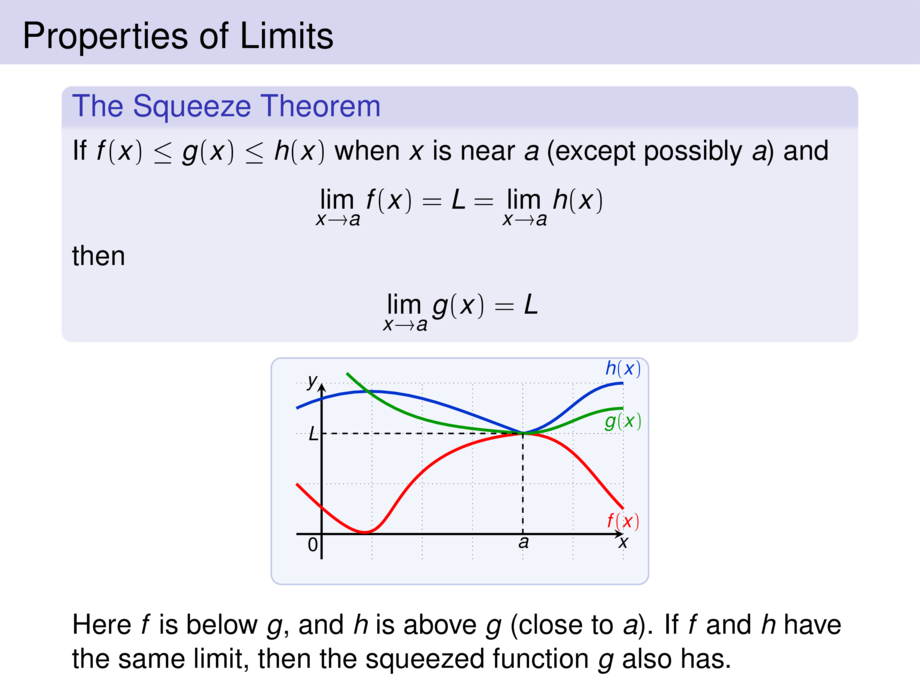
  Here $f$ is below $g$, and $h$ is above $g$ (close to $a$). 
  If $f$ and $h$ have the same limit, then the squeezed function $g$ also has.
  \vspace{10cm}
\end{frame}