







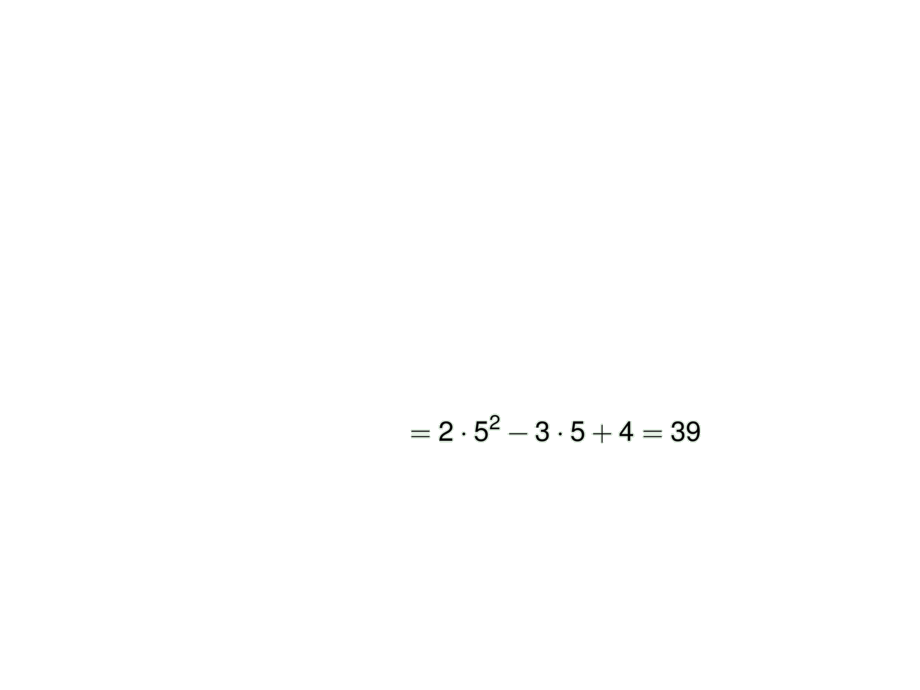



























































































68/145
\begin{frame}
\frametitle{Computing Limits: Direct Substitution Property}
\begin{block}{Direct Substitution Property}
If $f$ is a polynomial or a rational and $a$ is in the domain of $f$,
then:
\begin{talign}
\lim_{x\to a} f(x) = f(a)
\end{talign}
\end{block}
\pause
Works also for one-sided limits $\lim_{x\to a^{\pm}} f(x) = f(a)$.\\
\pause
Works also for algebraic functions if $f(x)$ is defined close to $a$.
% Functions for which $\lim_{x\to a} f(x) = f(a)$ are called continuous at $a$.\hspace*{-1ex}
% (we will study them in one of the following lectures)
\pause\bigskip
\begin{exampleblock}{}
The function $f(x) = 2x^2 - 3x + 4$ \pause is a polynomial and hence:\pause
\begin{talign}
\lim_{x \to 5} f(x) \mpause[1]{= f(5)} \mpause[2]{= 2\cdot 5^2 - 3\cdot 5 + 4 = 39}
\end{talign}
\end{exampleblock}
\pause\pause\pause\medskip
\begin{exampleblock}{}
The function $g(x) = \frac{x^3 + 2x^2 -1}{5-3x}$ \pause is rational and $-2$ is in the domain; hence:\pause
\begin{talign}
\lim_{x \to -2} g(x) \mpause[1]{= g(-2) }\mpause[2]{= \frac{(-2)^3 + 2\cdot (-2)^2 - 1}{5-3\cdot (-2)} = -\frac{1}{11}}
\end{talign}
\end{exampleblock}
\end{frame}

