


































































































21/145
\begin{frame}
\frametitle{Calculating Limits using Limit Laws}
\begin{block}{}
\begin{enumerate}
\item $\lim_{x\to a} \;[f(x) + g(x)] = \lim_{x\to a} f(x) + \lim_{x\to a} g(x)$
\item $\lim_{x\to a} \;[f(x) - g(x)] = \lim_{x\to a} f(x) - \lim_{x\to a} g(x)$
\item $\lim_{x\to a} \;[c \cdot f(x)] = c \cdot \lim_{x\to a} f(x)$
\item $\lim_{x\to a} \;[f(x) \cdot g(x)] = \lim_{x\to a} f(x) \cdot \lim_{x\to a} g(x)$
\item $\lim_{x\to a} \frac{f(x)}{g(x)} = \frac{\lim_{x\to a} f(x)}{\lim_{x\to a} g(x)}$ if $\lim_{x\to a} g(x) \ne 0$
\end{enumerate}
\end{block}
\bigskip
\begin{indentation}{-.2cm}{-1cm}
\begin{minipage}{.44\textwidth}
\scalebox{.6}{
\begin{tikzpicture}[default]
\diagram{-3}{3}{-2}{3}{1}
\diagramannotatez
\diagramannotatex{-3,-2,-1,1,2}
\diagramannotatey{-1,1,2}
\draw[cred,ultra thick] plot[smooth,domain=-3:-2,samples=20] function{2-(x+2)**2};
\draw[cred,ultra thick] (-2,2) to[out=-45,in=180,looseness=2] (1,2) to[out=0,in=135,looseness=1] node [at end,below] {$f(x)$} (3,.5);
\draw[cblue,ultra thick] (-3,-2/3) to (1,-2);
\draw[cblue,ultra thick] (1,-1) to node[at end,above] {$g(x)$} (3,1);
\node[exclude={cred}] at (-2,2) {};
\node[include={cred}] at (-2,3) {};
\node[exclude={cblue}] at (1,-1) {};
\node[include={cblue}] at (1,-2) {};
\end{tikzpicture}
}
\end{minipage}
\begin{minipage}{.65\textwidth}
\pause
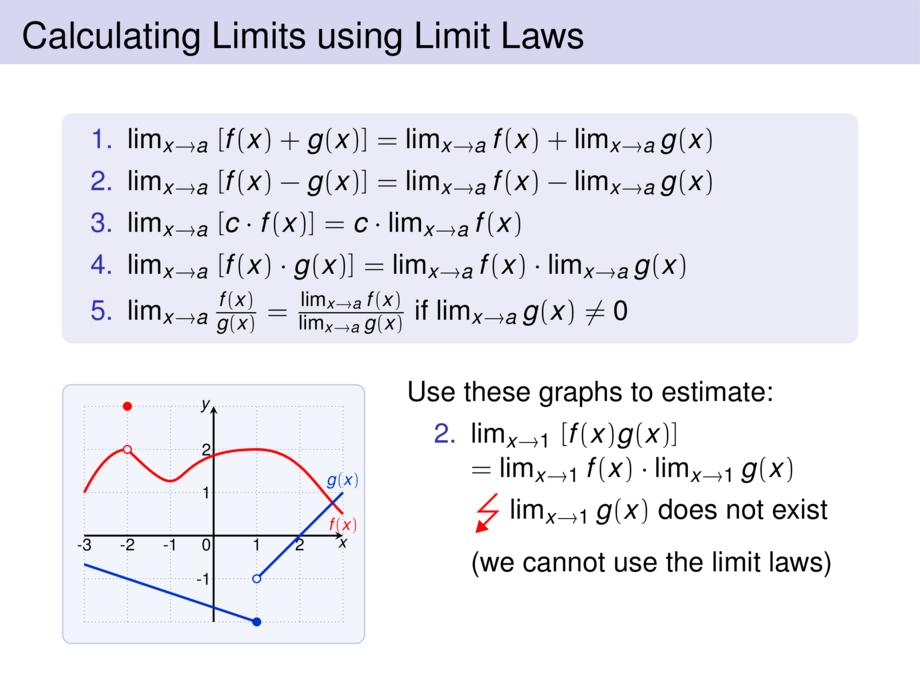
Use these graphs to estimate:\\[-1ex]
\pause
\begin{overlayarea}{\textwidth}{3.5cm}%
\only<-7>{%
\begin{itemize}
\item[1.] $\lim_{x\to -2}\; [f(x) + 5g(x)]$\\ \pause
$= \lim_{x\to -2} f(x) + \lim_{x\to -2} \;[5g(x)]$\\ \pause
$= \lim_{x\to -2} f(x) + 5\, \lim_{x\to -2} g(x)$\\ \pause
$= 2 + 5(-1)$\\ \pause
$= -3$
\end{itemize}
}
\pause[8]
\only<8-11>{%
\begin{itemize}
\item[2.] $\lim_{x\to 1}\; [f(x)g(x)]$\\\pause
$= \lim_{x\to 1} f(x) \cdot \lim_{x\to 1} g(x)$\\\pause\smallskip
\flash $\lim_{x\to 1} g(x)$ does not exist\\[1ex]\pause
(we cannot use the limit laws)
\end{itemize}
}
\pause[12]
\only<12-20>{%
\begin{itemize}
\item[2a.] $\lim_{x\to 1^-}\; [f(x)g(x)]$\\\pause
$= \lim_{x\to 1^-} f(x) \cdot \lim_{x\to 1^-} g(x)$\\\pause
$= 2 \cdot -2 $\pause $= -4$\pause
\item[2b.] $\lim_{x\to 1^+}\; [f(x)g(x)]$\\\pause
$= \lim_{x\to 1^+} f(x) \cdot \lim_{x\to 1^+} g(x)$\\\pause
$= 2 \cdot -1 $\pause $= -2$\pause
\item[$\implies$] $\lim_{x\to 1}\; [f(x)g(x)]$ does not exist
\end{itemize}
}
\pause[21]
\only<21-24>{%
\begin{itemize}
\item[3.] $\lim_{x\to 2}\; \frac{f(x)}{g(x)}$\pause
\ $ = \frac{\lim_{x\to 2} f(x)}{\lim_{x\to 2} g(x)}$\\\pause
\flash $\lim_{x\to 2} g(x) = 0$\\[1ex]\pause
(we cannot use the limit laws)
\end{itemize}
}
\pause[25]
\only<25-30>{%
\noindent Lets try without limit laws:
\begin{itemize}
\item[3a.] $\lim_{x\to 2^-}\; \frac{f(x)}{g(x)}$\pause
\ $ = -\infty$\\\pause
since $\lim_{x\to 2^-} f(x) \approx 1.6$, and\\
$g(x)$ approaches $0$, $g(x) < 0$\pause
\item[3b.] $\lim_{x\to 2^+}\; \frac{f(x)}{g(x)}$\pause
\ $ = \infty$\\\pause
since $\lim_{x\to 2^+} f(x) \approx 1.6$, and\\
$g(x)$ approaches $0$, $g(x) > 0$
\end{itemize}
}
\end{overlayarea}
\end{minipage}
\end{indentation}
\end{frame}

