


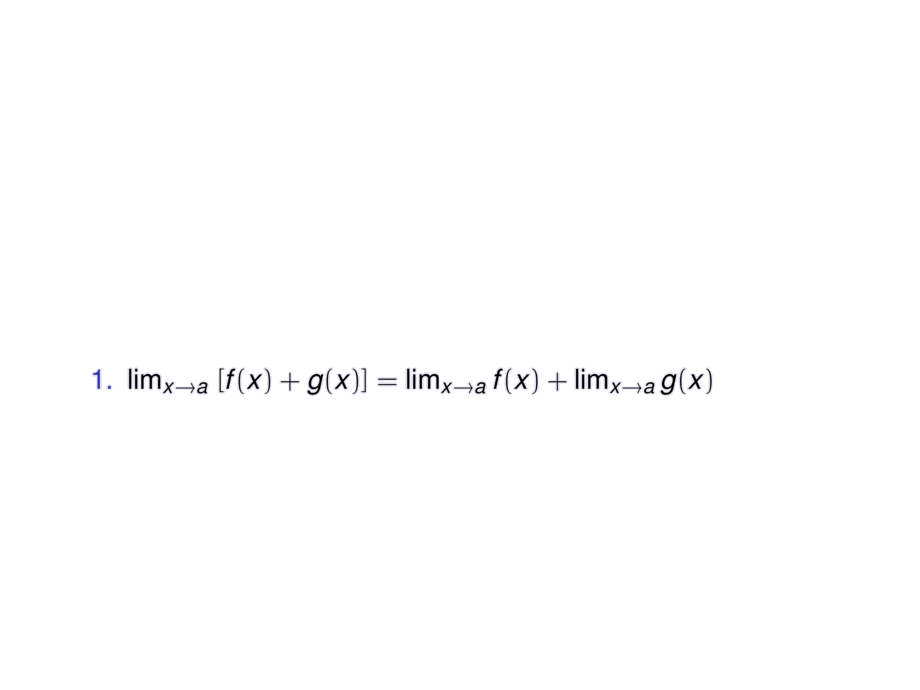































































































9/145
\begin{frame}
\frametitle{Calculating Limits using Limit Laws}
\begin{alertblock}{}
We have seen that calculating limits with a calculator sometimes leads to incorrect results.
\end{alertblock}
\pause\bigskip
We will now see how to compute limits using \emph{Limit Laws}:
\pause
\begin{block}{}
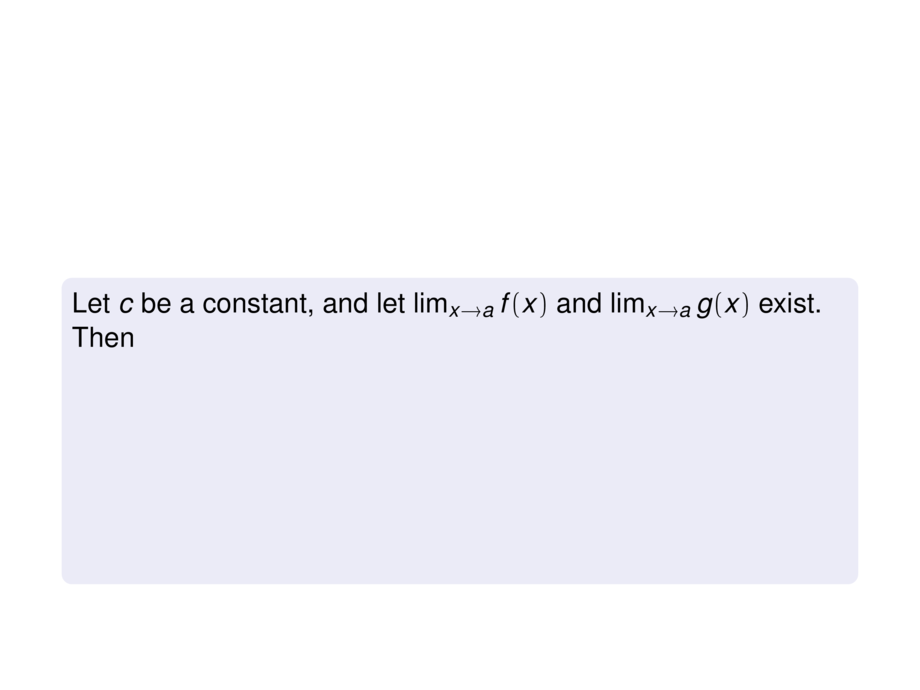
Let $c$ be a constant, and let $\lim_{x\to a} f(x)$ and $\lim_{x\to a} g(x)$ exist.
Then
\begin{enumerate}
\pause
\item $\lim_{x\to a} \;[f(x) + g(x)] = \lim_{x\to a} f(x) + \lim_{x\to a} g(x)$
% \\ \textcolor{gray}{(The limit of the sum is the sum of the limits)}
\pause
\item $\lim_{x\to a} \;[f(x) - g(x)] = \lim_{x\to a} f(x) - \lim_{x\to a} g(x)$
% \\ \textcolor{gray}{(The limit of the difference is the difference of the limits)}
\pause
\item $\lim_{x\to a} \;[c \cdot f(x)] = c \cdot \lim_{x\to a} f(x)$
\pause
\item $\lim_{x\to a} \;[f(x) \cdot g(x)] = \lim_{x\to a} f(x) \cdot \lim_{x\to a} g(x)$
% \\ \textcolor{gray}{(The limit of a product is the product of the limits)}
\pause
\item $\lim_{x\to a} \frac{f(x)}{g(x)} = \frac{\lim_{x\to a} f(x)}{\lim_{x\to a} g(x)}$ if $\lim_{x\to a} g(x) \ne 0$
\end{enumerate}
\end{block}
\bigskip\pause
These laws also work for one-sided limits $\lim_{x\to a^\pm}$.
\end{frame}

