\begin{frame}
  \frametitle{Infinite Limits}

  \begin{exampleblock}{}
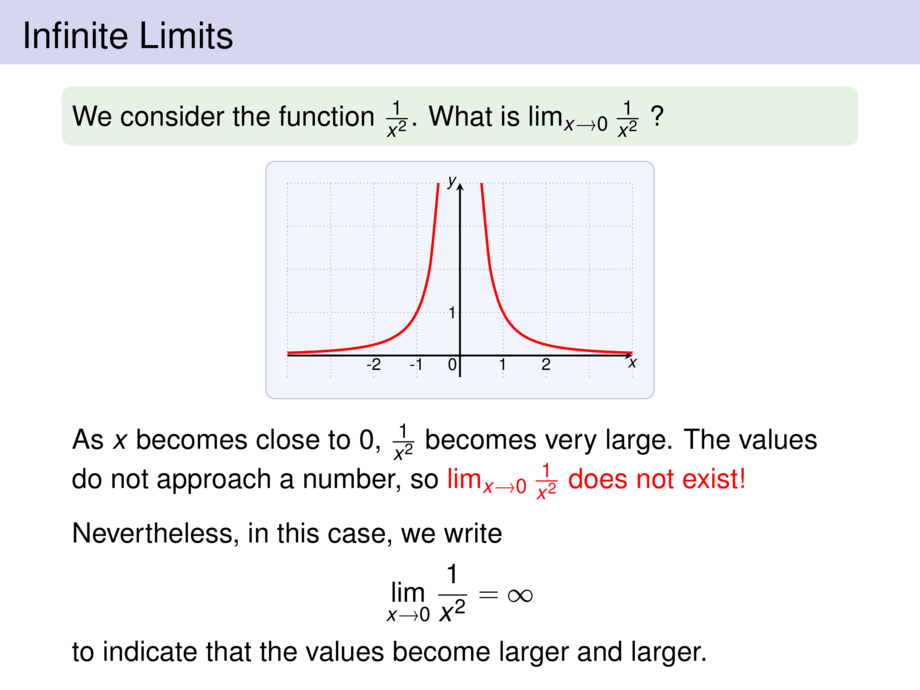
    We consider the function $\frac{1}{x^2}$. What is $\lim_{x\to 0} \frac{1}{x^2}$ ?
  \end{exampleblock}
  
  \begin{center}
    \scalebox{.6}{
    \begin{tikzpicture}[default]
      \diagram{-4}{4}{-.5}{4}{1}
      \diagramannotatez
      \diagramannotatex{-2,-1,1,2}
      \diagramannotatey{1}
      \draw[cred,ultra thick] plot[smooth,domain=-4:-0.5,samples=20] function{1/(x**2)};
      \draw[cred,ultra thick] plot[smooth,domain=0.5:4,samples=20] function{1/(x**2)};
    \end{tikzpicture}
    }
  \end{center}
  \pause
  
  As $x$ becomes close to $0$, $\frac{1}{x^2}$ becomes very large.
  \pause
  The values do not approach a number, so \alert{$\lim_{x\to 0} \frac{1}{x^2}$ does not exist!}
  \pause\bigskip
  
  Nevertheless, in this case, we write
  \begin{talign}
    \lim_{x\to 0} \frac{1}{x^2} = \infty
  \end{talign}
  to indicate that the values become larger and larger.
  \vspace{1cm}
\end{frame}