\begin{frame}
  \frametitle{Limit: Continued}
  
  \begin{block}{}
    $\lim_{x\to a} f(x) = L$
    if we can make the values of $f(x)$ arbitrarily close to $L$
    by taking $x$ sufficiently close to $a$ but not equal to $a$.
  \end{block}
  \medskip
  \pause
    
  Note that we never consider $f(x)$ for $x=a$. \alert{The value of $f(a)$ does not matter.}
  In fact, $f(x)$ need not be defined for $x=a$.
  \bigskip
  \pause

  \begin{indentation}{-.35cm}{-.5cm}
  \begin{minipage}{.35\textwidth}
  \begin{center}
  \scalebox{.5}{
  \begin{tikzpicture}[default,nodes={scale=1.4}]
    \diagram{-1}{5}{-1}{5}{1}
    \draw[cblue,ultra thick] plot[smooth,domain=-.8:4.5,samples=20] function{.2*x**3 - 1.0*(x+1)**2 + 3.4*x +2};

    \def\x{3.5}
    \def\y{{.2*\x^3 - 1.0*(\x+1)^2 + 3.4*\x +2}}
    \begin{scope}[dashed,cred,ultra thick,inner sep=1mm]
    \draw (\x,\y) -- (\x,-2mm) node [below] {a};
    \draw (\x,\y) -- (-2mm,\y) node [left] {$L$};
    \end{scope}
  \end{tikzpicture}
  }
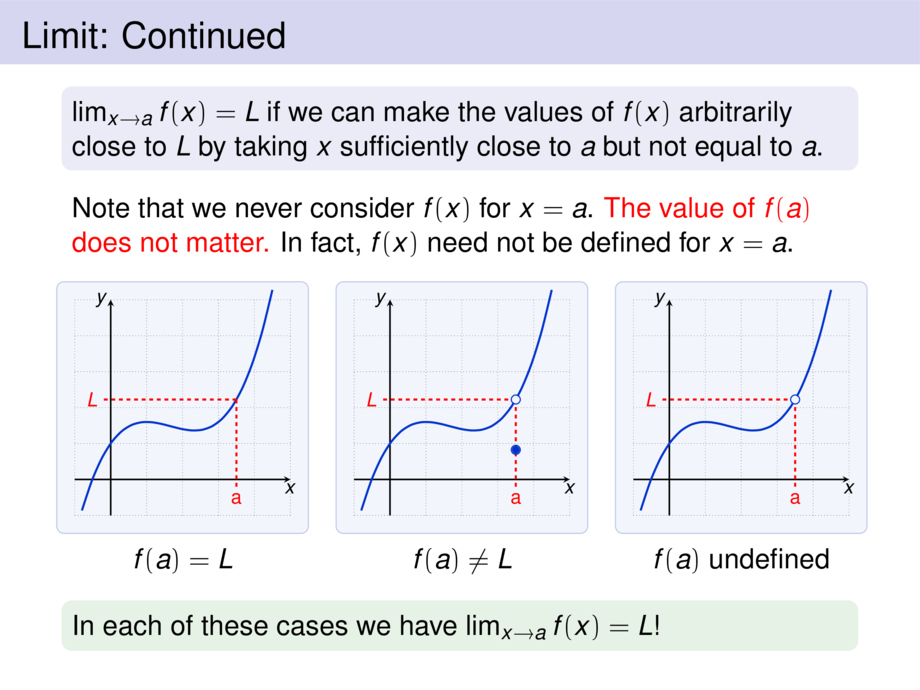
  $f(a) = L$
  \end{center}
  \end{minipage}
  %
  \begin{minipage}{.35\textwidth}
  \begin{center}
  \scalebox{.5}{
  \begin{tikzpicture}[default,nodes={scale=1.4}]
    \diagram{-1}{5}{-1}{5}{1}
    \draw[cblue,ultra thick] plot[smooth,domain=-.8:4.5,samples=20] function{.2*x**3 - 1.0*(x+1)**2 + 3.4*x +2};

    \def\x{3.5}
    \def\y{{.2*\x^3 - 1.0*(\x+1)^2 + 3.4*\x +2}}
    \begin{scope}[dashed,cred,ultra thick,inner sep=1mm]
    \draw (\x,\y) -- (\x,-2mm) node [below] {a};
    \draw (\x,\y) -- (-2mm,\y) node [left] {$L$};
    \end{scope}
    \node[exclude={cblue}] at (\x,\y) {};
    \node[include={cblue},yshift=-10mm] at (\x,\y) {};
  \end{tikzpicture}
  }
  $f(a) \ne L$
  \end{center}
  \end{minipage}
  %
  \begin{minipage}{.35\textwidth}
  \begin{center}
  \scalebox{.5}{
  \begin{tikzpicture}[default,nodes={scale=1.4}]
    \diagram{-1}{5}{-1}{5}{1}
    \draw[cblue,ultra thick] plot[smooth,domain=-.8:4.5,samples=20] function{.2*x**3 - 1.0*(x+1)**2 + 3.4*x +2};

    \def\x{3.5}
    \def\y{{.2*\x^3 - 1.0*(\x+1)^2 + 3.4*\x +2}}
    \begin{scope}[dashed,cred,ultra thick,inner sep=1mm]
    \draw (\x,\y) -- (\x,-2mm) node [below] {a};
    \draw (\x,\y) -- (-2mm,\y) node [left] {$L$};
    \end{scope}
    \node[exclude={cblue}] at (\x,\y) {};
  \end{tikzpicture}
  }
  $f(a)$ undefined
  \end{center}
  \end{minipage}
  \end{indentation}
  \pause\medskip
  
  \begin{exampleblock}{}
  In each of these cases we have $\lim_{x\to a} f(x) = L$!
  \end{exampleblock}
  \vspace{10cm}
\end{frame}