\begin{frame}
  \frametitle{The Limit of a Function}
  
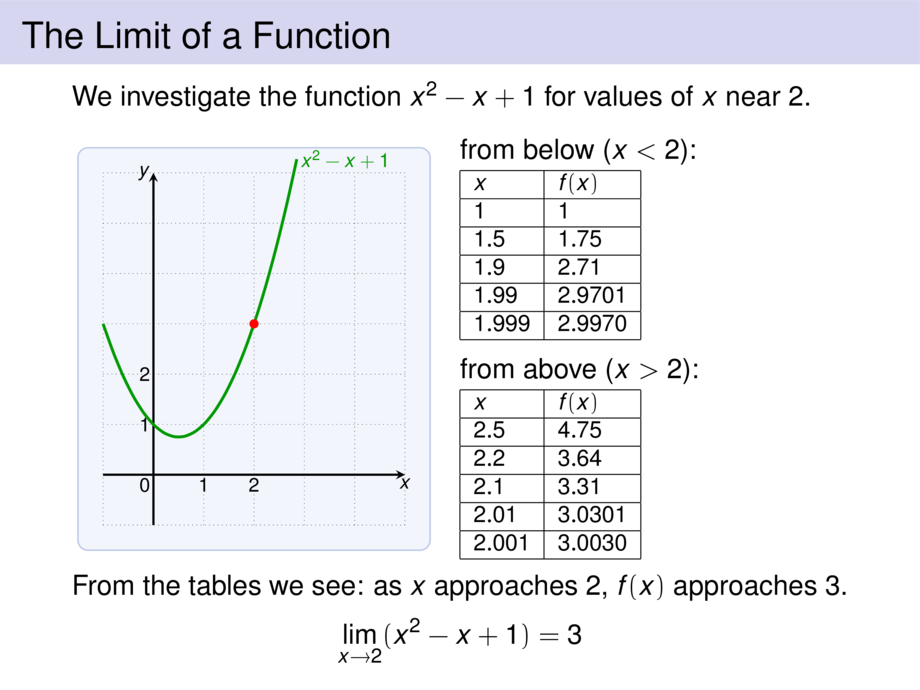
  We investigate the function $x^2-x+1$ for values of $x$ near $2$.
  \bigskip
  
  \begin{minipage}{.49\textwidth}
  \scalebox{.7}{
  \begin{tikzpicture}[default]
    \diagram{-1}{5}{-1}{6}{1}
    \diagramannotate
    \draw[ultra thick,cgreen] plot[smooth,domain=-1:2.85,samples=20] function{x**2-x+1} node[right] {$x^2-x+1$};

    \node[dot] (P) at (2,{2^2-2+1}) {};
  \end{tikzpicture}
  }
  \end{minipage}  
  \begin{minipage}{.49\textwidth}
    \pause
    from below ($x < 2$):\\[.2ex]
    \scalebox{.9}{\small
    \begin{tabular}{|l|l|}
      \hline
      $x$ & $f(x)$ \\
      \hline
      $1$ & $1$ \\
      \hline
      $1.5$ & $1.75$ \\
      \hline
%       $1.8$ & $2.44$ \\
%       \hline
      $1.9$ & $2.71$ \\
      \hline
      $1.99$ & $2.9701$ \\
      \hline
      $1.999$ & $2.9970$ \\
      \hline
    \end{tabular}
    }
    \medskip\pause
    
    from above ($x > 2$):\\[.2ex]
    \scalebox{.9}{\small
    \begin{tabular}{|l|l|}
      \hline
      $x$ & $f(x)$ \\
      \hline
%       $3$ & $7$ \\
%       \hline
      $2.5$ & $4.75$ \\
      \hline
      $2.2$ & $3.64$ \\
      \hline
      $2.1$ & $3.31$ \\
      \hline
      $2.01$ & $3.0301$ \\
      \hline
      $2.001$ & $3.0030$ \\
      \hline
    \end{tabular}
    }
  \end{minipage}
  \medskip\pause
  
  From the tables we see: as $x$ approaches $2$, $f(x)$ approaches $3$.
  \begin{talign}
    \lim_{x\to 2} (x^2 - x + 1) = 3
  \end{talign}
  
\end{frame}