


































































































11/154
\begin{frame}
\frametitle{The Tangent: Example}
\begin{exampleblock}{}
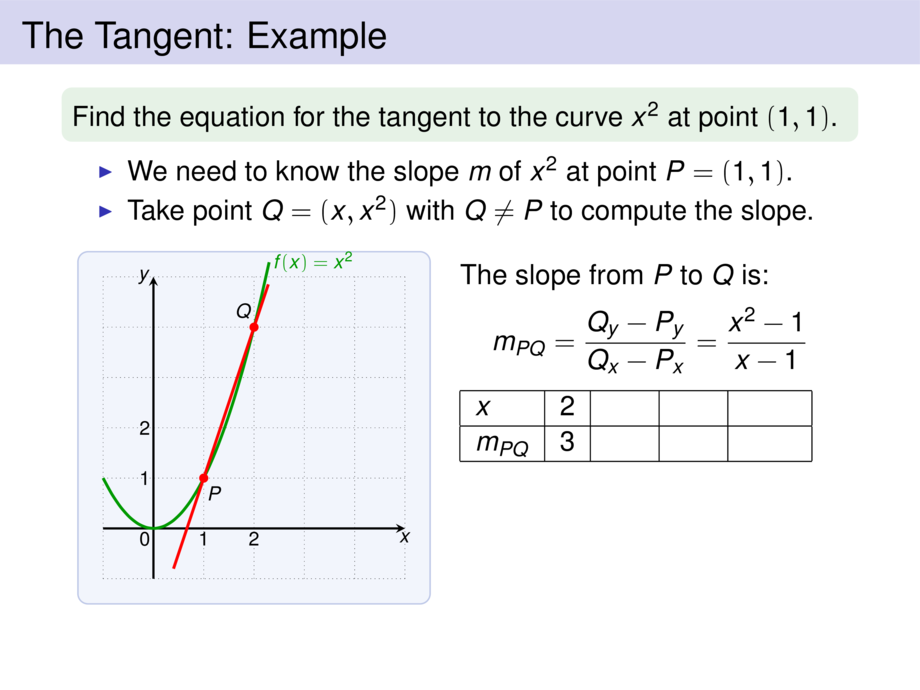
Find the equation for the tangent to the curve $x^2$ at point $(1,1)$.
\end{exampleblock}
\vspace{-.5ex}
\begin{itemize}
\item<2-> We need to know the slope $m$ of $x^2$ at point $P = (1,1)$.
\item<3-> Take point $Q = (x,x^2)$ with $Q \ne P$ to compute the slope.
\end{itemize}
\medskip
\begin{minipage}{.49\textwidth}
\scalebox{.7}{
\begin{tikzpicture}[default]
\diagram{-1}{5}{-1}{5}{1}
\diagramannotate
\draw[name path=x2,ultra thick,cgreen] plot[smooth,domain=-1:2.3,samples=20] function{x**2} node[right] {$f(x) =x^2$};
\node[dot] (P) at (1,{1^2}) {};
\node[anchor=north west,at=(P.south)] {$P$};
\onslide<18->{\tangent[ultra thick]{55}{80}{\x^2}{1}}
\foreach \s/\x in {4/2,5/2,6/2,7/2,8/2,9/2,10/1.5,11/1.5,12/1.1,13/1.1,14/1.01,15/1.01,16/1.01,17/1.01} {
\only<\s>{
\node[dot] (Q) at (\x,{\x^2}) {};
\node[anchor=south east,at=(Q.north)] {$Q$};
\through[red,ultra thick]{2cm}{(1cm+(2-\x)*3cm)}{P}{Q}
}
}
\end{tikzpicture}
}
\end{minipage}
%
\pause\pause\pause\pause%
\begin{minipage}{.49\textwidth}
% Take $Q = (x,x^2)$ with $Q \ne P$.
The slope from $P$ to $Q$ is:
\begin{talign}
m_{PQ} = \frac{Q_y - P_y}{Q_x - P_x} \onslide<6->{= \frac{x^2 - 1}{x - 1}}
\end{talign}
\pause\pause
\begin{tabular}{|l|l|l|l|l|}
\hline
$x$ & \onslide<8->{$2$} & \onslide<10->{$1.5$} & \onslide<12->{$1.1$} & \onslide<14->{$1.01$} \\
\hline
$m_{PQ}$ & \onslide<9->{$3$} & \onslide<11->{$2.5$} & \onslide<13->{$2.1$} & \onslide<15->{$2.01$} \\
\hline
\end{tabular}\pause[16]~\ldots
\bigskip\pause
The closer $Q$ to $P$, the closer $m_{PQ}$ gets to $2$. \pause
\structure{Suggests that in $P$ the slope $m = 2$.}
\end{minipage}
\bigskip\pause
Thus the \alert{tangent is $y - 1 = 2(x - 1)$} \pause or \alert{$y = 2x - 1$}.
\bigskip
\end{frame}

