\begin{frame}
  \frametitle{Inverse Trigonometric Functions}

  \begin{minipage}{.49\textwidth}
  \begin{center}
  \scalebox{.8}{
  \begin{tikzpicture}[default,baseline=0cm]
    \diagram{-1.5}{1.5}{-1.1}{1.3}{1}
    \begin{scope}[ultra thick]
    \draw[cred] plot[smooth,domain=-1:1,samples=300] (\x,{sin(\x*90)});
    \end{scope}
    \diagramannotatez
    \diagramannotatexx{-1/$-\frac{\pi}{2}$,1/$\frac{\pi}{2}$}
    \diagramannotatey{1,-1}
  \end{tikzpicture}
  }\\[.5ex]
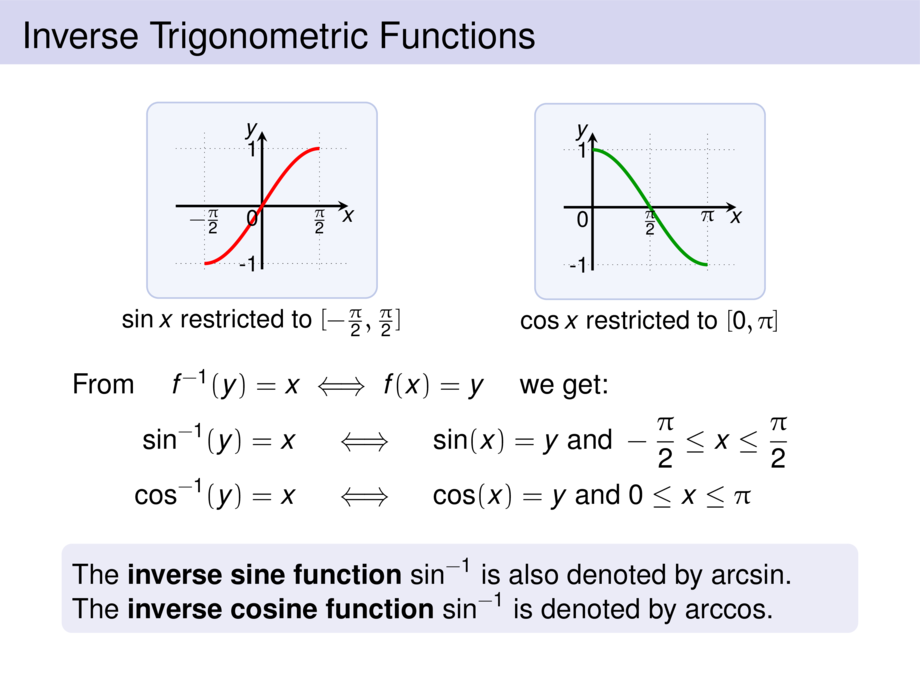
  {\small $\sin x$ restricted to $[-\frac{\pi}{2},\frac{\pi}{2}]$}
  \end{center}
  \end{minipage}
  \begin{minipage}{.49\textwidth}
  \begin{center}
  \scalebox{.8}{
  \begin{tikzpicture}[default,baseline=0cm]
    \diagram{-.5}{2.5}{-1.1}{1.3}{1}
    \begin{scope}[ultra thick]
    \draw[cgreen] plot[smooth,domain=0:2,samples=300] (\x,{cos(\x*90)});
    \end{scope}
    \diagramannotatez
    \diagramannotatexx{1/$\frac{\pi}{2}$,2/$\pi$}
    \diagramannotatey{1,-1}
  \end{tikzpicture}
  }\\[.5ex]
  {\small $\cos x$ restricted to $[0,\pi]$}  
  \end{center}
  \end{minipage}
  \pause\bigskip
  
  From \quad $f^{-1}(y) = x \iff f(x) = y$ \quad we get:\pause
  \begin{talign}
    \sin^{-1}(y) = x \quad&\iff\quad \sin(x) = y \text{ and } -\frac{\pi}{2} \le x \le \frac{\pi}{2}\\
    \mpause[1]{\cos^{-1}(y) = x} \quad&\mpause[1]{\iff\quad \cos(x) = y \text{ and } 0 \le x \le \pi}
  \end{talign}
  \pause\vspace{-2ex}
  
  \begin{block}{}
    The \emph{inverse sine function} $\sin^{-1}$ is also denoted by $\arcsin$.\\\pause
    The \emph{inverse cosine function} $\sin^{-1}$ is denoted by $\arccos$.
  \end{block}  
\end{frame}