\begin{frame}
  \frametitle{Inverse Functions}

  \begin{block}{}
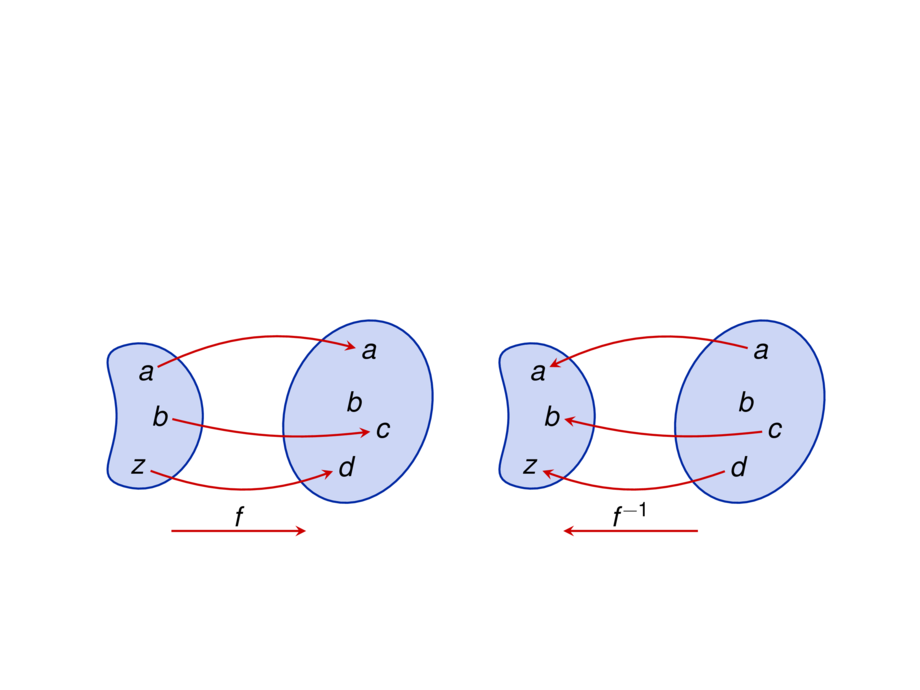
    A function $g$ is the inverse of a function $f$ if
    \begin{talign}
      g(f(x)) = x \quad \text{for all $x$ in the domain of $f$}
    \end{talign}
    (and the domain of $g$ is the range of $f$).
  \end{block}
  \pause\medskip
  
  \begin{minipage}{.50\textwidth}
  \begin{center}
    \begin{tikzpicture}[default]
      \draw [fill=cblue!20,draw=cdblue] (0cm,0cm) to[out=10,in=90] (1cm,-1cm) to[out=-90,in=-10] (0cm,-2cm) to[out=170,in=-90,looseness=1.5] (-.2cm,-1cm) to[out=90,in=190,looseness=1.5] (0,0);
      \node (D) at (0,-2.6cm) {};
      \node (x) at (.2cm,-.4cm) {$a$}; 
      \node (a) at (.4cm,-1cm) {$b$}; 
      \node (z) at (.1cm,-1.7cm) {$z$}; 
      \begin{scope}[xshift=35mm]
      \draw [fill=cblue!20,draw=cdblue,rotate=-20] (0cm,-1cm) ellipse (1cm and 1.3cm);
      \node (E) at (-.5,-2.6cm) {};
      \node (a') at (-.2cm,-.1cm) {$a$}; 
      \node (c') at (-.4cm,-.8cm) {$b$}; 
      \node (q') at (-.5cm,-1.7cm) {$d$}; 
      \node (p') at (-0cm,-1.2cm) {$c$}; 
      \end{scope}
      \begin{scope}[cdred,->,>=stealth,thick]
      \draw (x) to[bend left=20] (a');
      \draw (a) to[bend left=-10] (p');
      \draw (z) to[bend left=-20] (q');
      \draw [shorten >= 5mm, shorten <= 5mm] (D) to node [above,black] {$f$} (E);
      \end{scope}
    \end{tikzpicture}
  \end{center}
  \end{minipage}
  \begin{minipage}{.49\textwidth}
  \begin{center}
    \begin{tikzpicture}[default]
      \draw [fill=cblue!20,draw=cdblue] (0cm,0cm) to[out=10,in=90] (1cm,-1cm) to[out=-90,in=-10] (0cm,-2cm) to[out=170,in=-90,looseness=1.5] (-.2cm,-1cm) to[out=90,in=190,looseness=1.5] (0,0);
      \node (D) at (0,-2.6cm) {};
      \node (x) at (.2cm,-.4cm) {$a$}; 
      \node (a) at (.4cm,-1cm) {$b$}; 
      \node (z) at (.1cm,-1.7cm) {$z$}; 
      \begin{scope}[xshift=35mm]
      \draw [fill=cblue!20,draw=cdblue,rotate=-20] (0cm,-1cm) ellipse (1cm and 1.3cm);
      \node (E) at (-.5,-2.6cm) {};
      \node (a') at (-.2cm,-.1cm) {$a$}; 
      \node (c') at (-.4cm,-.8cm) {$b$}; 
      \node (q') at (-.5cm,-1.7cm) {$d$}; 
      \node (p') at (-0cm,-1.2cm) {$c$}; 
      \end{scope}
      \begin{scope}[cdred,<-,>=stealth,thick]
      \draw (x) to[bend left=20] (a');
      \draw (a) to[bend left=-10] (p');
      \draw (z) to[bend left=-20] (q');
      \draw [shorten >= 5mm, shorten <= 5mm] (D) to node [above,black] {$f^{-1}$} (E);
      \end{scope}
    \end{tikzpicture}
  \end{center}
  \end{minipage}
  \pause\bigskip

  A function $f$ has an inverse if and only if $f$ is one-to-one.
\end{frame}