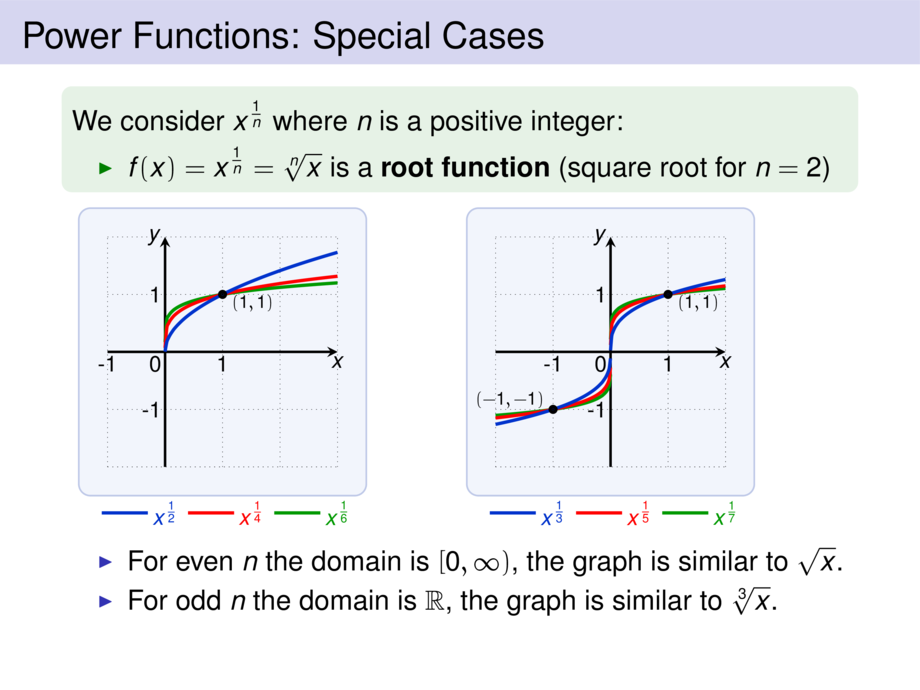


































































































41/353
\begin{frame}
\frametitle{Power Functions: Special Cases}
\begin{exampleblock}{}
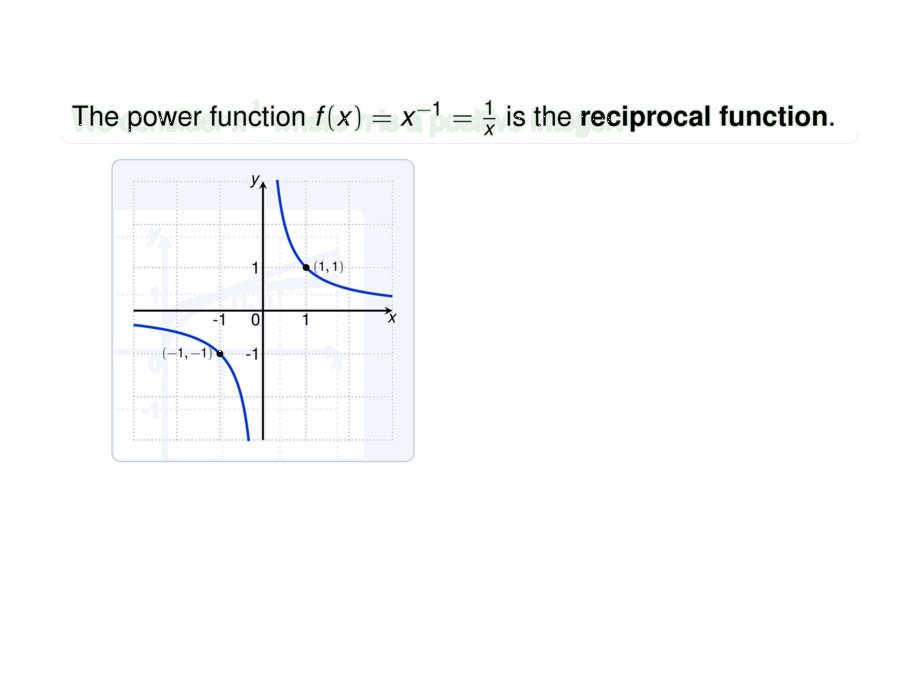
The power function $f(x) = x^{-1} = \frac{1}{x}$ is the \emph{reciprocal function}.
\end{exampleblock}
\begin{center}
\begin{minipage}{.49\textwidth}
\scalebox{.6}{
\begin{tikzpicture}[default,baseline=1cm]
\diagram{-3}{3}{-3}{3}{1}
\diagramannotatez
\diagramannotatex{-1,1}
\diagramannotatey{-1,1}
\begin{scope}[ultra thick]
\draw[cblue] plot[smooth,domain=0.33:3,samples=100] (\x,{1/\x});
\draw[cblue] plot[smooth,domain=-3:-0.33,samples=100] (\x,{1/\x});
\node (a) [include=black,minimum size=1mm] at (1,1) {};
\node[r=(a)] {$(1,1)$};
\node (b) [include=black,minimum size=1mm] at (-1,-1) {};
\node[l=(b)] {$(-1,-1)$};
\end{scope}
\end{tikzpicture}
}
\end{minipage}
\onslide<3->{
\begin{minipage}{.40\textwidth}
\scalebox{.6}{
\begin{tikzpicture}[default,baseline=1cm]
{\def\diax{P}
\def\diay{V}
\diagram{-1}{5}{-1}{5}{1}}
\diagramannotatez
\begin{scope}[ultra thick]
\draw[cblue] plot[smooth,domain=0.4:5,samples=100] (\x,{2/\x});
\end{scope}
\end{tikzpicture}
}
\end{minipage}
}
\end{center}
\pause\smallskip
\begin{exampleblock}{}
This function arises in physics and chemistry. E.g. Boyle's law
says that, when the temperature is constant, then the volume $V$ of a gas
is inversely proportional to the pressure $P$:
\begin{malign}
V = \frac{C}{P} &&\text{where $C$ is a constant}
\end{malign}
\end{exampleblock}
\vspace{10cm}
\end{frame}

