\begin{frame}{Example}
  \begin{exampleblock}{}
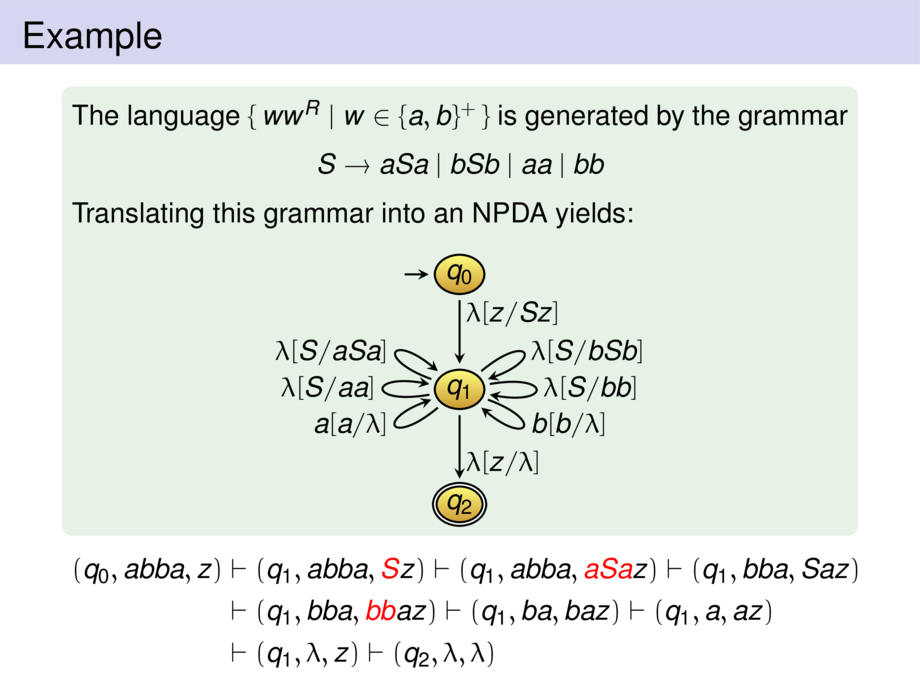
    The language $\{\, ww^R \mid w\in\{a,b\}^+ \,\}$ is generated by the grammar
    \begin{talign}
      S \to aSa \mid bSb \mid aa \mid bb
    \end{talign}
    \pause
    Translating this grammar into an NPDA yields:
    \pause
    \begin{center}
    \begin{tikzpicture}[default,node distance=16mm,->,s/.style={minimum size=5mm}]
      \node (q0) [state,s] {$q_0$}; \draw ($(q0) + (-8mm,0mm)$) -- (q0); 
      \node (q1) [state,s,below of=q0] {$q_1$};
      \node (q2) [fstate,s,below of=q1] {$q_2$};
  
      \mpause[1]{ \draw (q0) to node [label,right,pos=.25] {$\lambda[z/Sz]$} (q1); }
      
      \mpause{
      \draw (q1) to[out=150+10,in=150-10,looseness=17] node [rectangle,left,label,inner sep=1mm] {$\lambda[S/aSa]$} (q1);
      \draw (q1) to[out=180+10,in=180-10,looseness=17] node [rectangle,left,label,inner sep=1mm] {$\lambda[S/aa]$} (q1);

      \draw (q1) to[out=30+10,in=30-10,looseness=17] node [rectangle,right,label,inner sep=1mm] {$\lambda[S/bSb]$} (q1);
      \draw (q1) to[out=0+10,in=0-10,looseness=17] node [rectangle,right,label,inner sep=1mm] {$\lambda[S/bb]$} (q1);
      }

      \mpause{
      \draw (q1) to[out=210+10,in=210-10,looseness=17] node [rectangle,left,label,inner sep=1mm] {$a[a/\lambda]$} (q1);
      \draw (q1) to[out=-30+10,in=-30-10,looseness=17] node [rectangle,right,label,inner sep=1mm] {$b[b/\lambda]$} (q1);
      }
      
      \mpause{
      \draw (q1) to node [label,right,pos=.75] {$\lambda[z/\lambda]$} (q2);
      }
    \end{tikzpicture}
    \end{center}
  \end{exampleblock}
  \pause\pause\pause\pause\pause\vspace{-2ex}
  \begin{malign}
  (q_0,abba,z) 
  &\mpause[1]{\vdash (q_1,abba,\alert{S}z) } 
   \mpause{\vdash (q_1,abba,\alert{aSa}z) }
   \mpause{\vdash (q_1,bba,Saz)} \\
  &\mpause{\vdash (q_1,bba,\alert{bb}az)} 
   \mpause{\vdash (q_1,ba,baz)}
   \mpause{\vdash (q_1,a,az)} \\
  &\mpause{\vdash (q_1,\lambda,z)}
   \mpause{\vdash (q_2,\lambda,\lambda)}
  \end{malign}
  \bigskip
\end{frame}