\begin{frame}{Pushdown Automata}
  Next to the input alphabet $\Sigma$, there is now a \emph{stack alphabet} $\Gamma$.
  \medskip
  
  \begin{block}{}
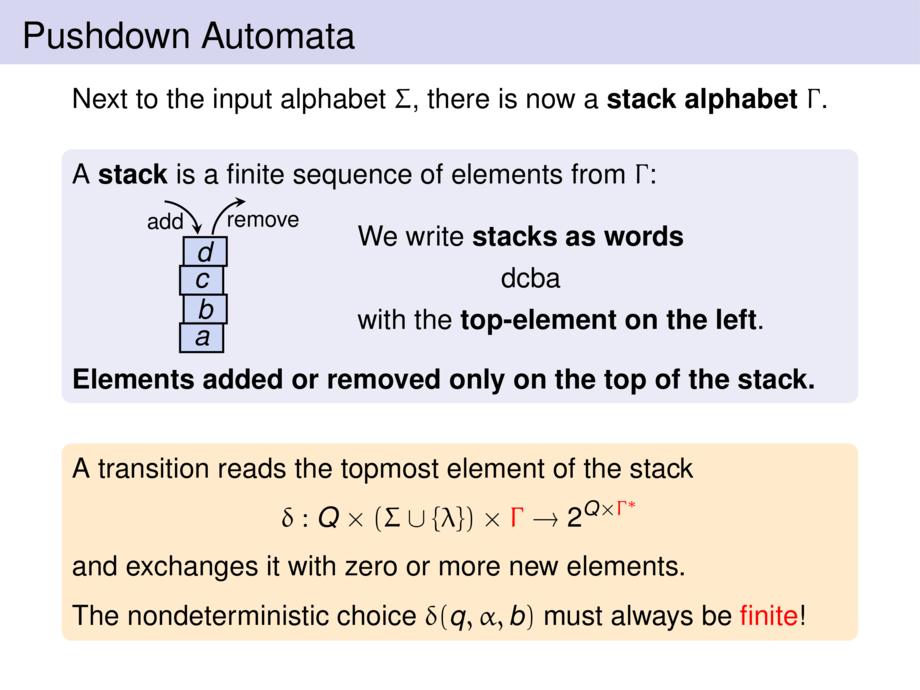
    A \emph{stack} is a finite sequence of elements from $\Gamma$:
    \begin{center}
      \vspace{-1ex}
      \begin{tikzpicture}[default,nodes={rectangle},n/.style={draw,minimum width=6mm,minimum height=4mm,fill=cblue!20},label/.style={scale=0.8}]
        \node (a) [n] at (0mm,0mm) {$a$};
        \node (b) [n] at (.5mm,4mm) {$b$};
        \node (c) [n] at (0mm,8mm) {$c$};
        \node (d) [n] at (.5mm,12mm) {$d$};
        \draw [<-] ($(d)+(-1mm,2mm)$) to[bend left=-40] node [left,label,pos=0.3,xshift=-1mm] {add} ++(-5mm,5mm);
        \draw [->] ($(d)+(1mm,2mm)$) to[bend left=40] node [right,label,pos=0.3,xshift=1mm] {remove} ++(5mm,5mm);
        
        \mpause[1]{\node [align=left] at (5cm,.8cm) {We write \emph{stacks as words}\\[.5ex]\hspace{2cm}dcba\\[.5ex]with the \emph{top-element on the left}.};}
      \end{tikzpicture}
      \vspace{-1.5ex}
    \end{center}
    \emph{Elements added or removed only on the top of the stack.}
  \end{block}
  \pause\pause\medskip
  
  \begin{goal}{}
    A transition reads the topmost element of the stack
    \begin{talign}
      \delta : Q \times (\Sigma \cup \{ \lambda \}) \times \alert{\Gamma} \to 2^{Q \times \alert{\Gamma^*}}
    \end{talign}
    and exchanges it with zero or more new elements.
    \pause\medskip
    
    The nondeterministic choice $\delta(q,\alpha,b)$ must always be \alert{finite}!
  \end{goal}
  \bigskip
\end{frame}