\begin{frame}{DFAs are Deterministic}
  Recall that $\delta$ is a function from $Q \times \Sigma$ to $Q$.
  \begin{goal}{}
    \emph{DFAs are deterministic:}
    \begin{itemize}
      \item []
    For every state $q\in Q$ and every symbol $a \in \Sigma$,
    the state $q$ has \emph{precisely one outgoing arrow} with label $a$.
    \end{itemize}
  \end{goal}
  \pause\medskip
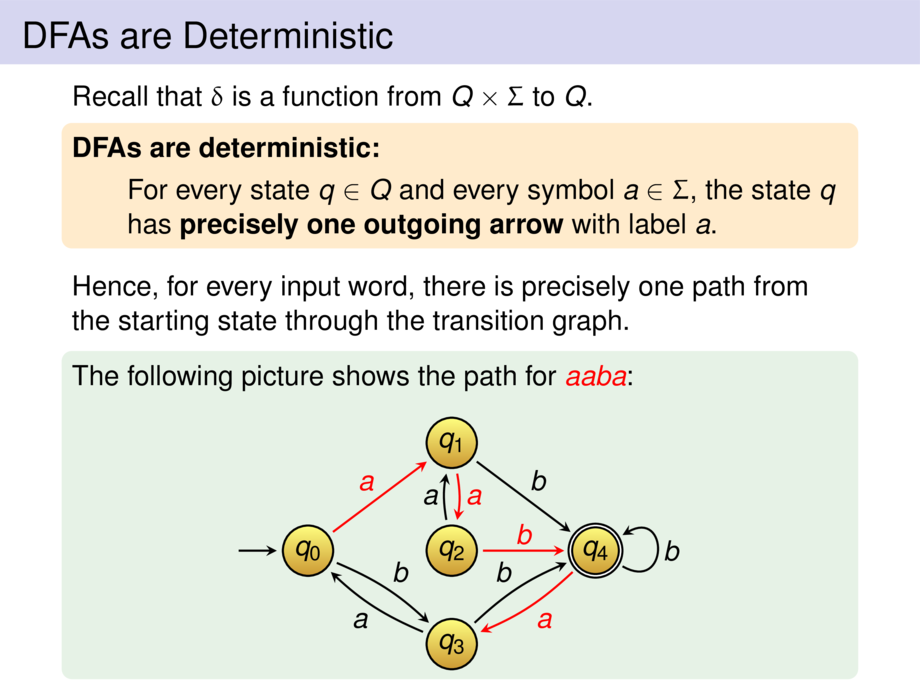
  Hence, for every input word, there is precisely one path 
  from the starting state through the transition graph.

  \begin{exampleblock}{}
    The following picture shows the path for \alert{$aaba$}:
    \begin{center}
      \begin{tikzpicture}[default,node distance=20mm,->]
        \node (q0) [state] {$q_0$}; \draw ($(q0) + (-10mm,0mm)$) -- (q0); 
        \node (q2) [state,right of=q0] {$q_2$};
        \node (q4) [fstate,right of=q2] {$q_4$};
        \begin{scope}[node distance=15mm]
        \node (q1) [state,above of=q2] {$q_1$};
        \node (q3) [state,below of=q2,node distance=13mm] {$q_3$};
        \end{scope}
        
        \draw [red] (q0) to node [label,above left] {$a$} (q1);
        \draw (q0) to[bend left=10] node [label,above right] {$b$} (q3);
        \draw [red] (q1) to[bend left=10] node [label,right] {$a$} (q2);
        \draw (q1) to node [label,above right] {$b$} (q4);
        \draw (q2) to[bend left=10] node [label,left] {$a$} (q1);
        \draw [red] (q2) to node [label,above] {$b$} (q4);
        \draw (q3) to[bend left=10] node [label,below left] {$a$} (q0);
        \draw (q3) to[bend left=10] node [label,above left] {$b$} (q4);
        \draw [red] (q4) to[bend left=10] node [label,below right] {$a$} (q3);
        \draw (q4) to[rloop] node [label,right] {$b$} (q4);
      \end{tikzpicture}
    \end{center}
  \end{exampleblock}
\end{frame}